Các phép biến hình là một chủ đề quan trọng trong chương trình Toán 11 hay gặp trong các bài thi THPT Quốc Gia. Vậy phép biến hình là gì? Kiến thức về các phép biến hình toán 11? Một số dạng bài tập các phép biến hình lớp 11?…. Trong nội dung bài viết dưới đây, DINHNGHIA.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề này nhé!
Định nghĩa phép biến hình là gì?
Định nghĩa phép biến hình
Phép biến hình trong mặt phẳng theo định nghĩa là một quy tắc để với mỗi điểm \ ( M \ ) thuộc mặt phẳng, ta xác lập được một điểm duy nhất \ ( M ’ \ ) thuộc mặt phẳng ấy. Điểm \ ( M ’ \ ) được gọi là ảnh của điểm \ ( M \ ) qua phép biến hình ấy
Ví dụ phép biến hình

Cho đường thẳng \ ( \ Delta \ ). Với mỗi điểm \ ( M \ ) ta xác lập \ ( M ’ \ ) là hình chiếu của \ ( M \ ) lên \ ( \ Delta \ ) thì ta được một phép biến hình. Phép biến hình này được gọi là phép chiếu vuông góc lên đường thẳng \ ( \ Delta \ )
***Chú ý: Với mỗi điểm \( M \) ta xác định điểm \( M’ \) trùng với \( M \) thì ta cũng được một phép biến hình. Phép biến hình đó được gọi là phép đồng nhất.
Ký hiệu và thuật ngữ

Lý thuyết các phép biến hình lớp 11
Phép dời hình là gì?
Phép dời hình theo định nghĩa là phép biến hình không làm biến hóa khoảng cách giữa hai điểm bất kể .
Tính chất của phép dời hình
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi khác thứ tự giữa ba điểm đó .
- Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó
- Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó .
- Biến đường tròn thành đường tròn có cùng nửa đường kính
Dưới đây là 1 số ít phép dời hình quan trọng :
Phép tịnh tiến
- Trong mặt phẳng cho véc tơ \ ( \ vec { v } \ neq 0 \ ). Phép biến hình biến mỗi điểm \ ( M \ ) thành điểm \ ( M ’ \ ) sao cho \ ( \ overrightarrow { MM ’ } = \ vec { v } \ ) được gọi là phép tịnh tiến theo véc tơ \ ( \ vec { v } \ )
- Kí hiệu : \ ( T_ { \ vec { v } } \ )
- Biểu thức tọa độ :
Trong mặt phẳng tọa độ \ ( Oxy \ ) cho \ ( M ( x ; y ) ; M ’ ( x ’ ; y ’ ) ; \ vec { v } = ( a ; b ) \ ). Khi đó nếu \ ( M ’ = T_ { \ vec { v } } ( M ) \ ) thì :
\ ( \ left \ { \ begin { matrix } x ’ = x + a \ \ y ’ = y + b \ end { matrix } \ right. \ )
Ví dụ:
Trong mặt phẳng \ ( Oxy \ ) cho véc tơ \ ( \ vec { u } = ( 1 ; 3 ) \ ) và đường thẳng \ ( d : 2 x – y + 3 = 0 \ ). Viết phương trình đường thẳng \ ( d ’ \ ) là ảnh của \ ( d \ ) qua phép tịnh tiến \ ( T_ { \ vec { u } } \ )
Cách giải:
Lấy \ ( M ( 0 ; – 3 ) \ ) là một điểm bất kỳ nằm trên \ ( d \ )
Gọi \ ( T_ { \ vec { u } } ( M ) = M ’ \ ). Khi đó \ ( M ’ ( 1 ; 0 ) \ )
Vì \ ( d ’ / / d \ Rightarrow d ’ : 2 x – y + c = 0 \ )
Vì \ ( M ‘ ( 1 ; 0 ) \ in d ’ \ Rightarrow c = – 2 \ )
Vậy phương trình \ ( d ’ : 2 x – y-2 = 0 \ )
Phép đối xứng trục
- Trong mặt phẳng cho đường thẳng \ ( d \ ). Phép biến hình biến mỗi điểm \ ( M \ ) thành điểm \ ( M ’ \ ) sao cho [ late ] d [ / latex ] là đường thẳng trung trực của \ ( MM ’ \ ) được gọi là phép đối xứng trục \ ( d \ )
- Kí hiệu : \ ( D_d \ )
- Biểu thức tọa độ :
Trong mặt phẳng tọa độ \ ( Oxy \ ) cho \ ( M ( x ; y ) ; M ’ ( x ’ ; y ’ ) \ ). Khi đó
Nếu \ ( M ’ = D_ { Ox } ( M ) \ ) thì \ ( \ left \ { \ begin { matrix } x ’ = x \ \ y ’ = – y \ end { matrix } \ right. \ )
Nếu \ ( M ’ = D_ { Oy } ( M ) \ ) thì \ ( \ left \ { \ begin { matrix } x ’ = – x \ \ y ’ = y \ end { matrix } \ right. \ )
Ví dụ:
Trong mặt phẳng \ ( Oxy \ ) cho đường thẳng \ ( d : x-2y+4 = 0 \ ) và điểm \ ( M ( 1 ; 5 ) \ ). Tìm ảnh \ ( M ’ \ ) của \ ( M \ ) qua phép đối xứng trục \ ( D_d \ )
Cách giải:
Vì \ ( d : x-2y+4 = 0 \ Rightarrow \ vec { u } ( 1 ; – 2 ) \ ) là véc tơ pháp tuyến của \ ( d \ )
\ ( \ Rightarrow \ vec { n } ( 2 ; 1 ) \ ) là véc tơ chỉ phương của \ ( d \ )
Vì \ ( d \ ) là trung trực của \ ( MM ’ \ Rightarrow \ vec { n } ( 2 ; 1 ) \ ) là véc tơ pháp tuyến của \ ( MM ’ \ )
Vậy \ ( \ Rightarrow MM ’ : 2 x + y-7 = 0 \ )
Gọi \ ( K = MM ’ \ cap d \ Rightarrow \ ) tọa độ \ ( K \ ) là nghiệm của hệ phương trình :
\ ( \ left \ { \ begin { matrix } x-2y+4 = 0 \ \ 2 x + y-7 = 0 \ end { matrix } \ right. \ Rightarrow \ left \ { \ begin { matrix } x = 2 \ \ y = 3 \ end { matrix } \ right. \ )
Vậy \ ( K ( 2 ; 3 ) \ ). Mặt khác, do \ ( K \ ) là trung điểm \ ( MM ’ \ ) nên \ ( \ Rightarrow M ’ = ( 3 ; 1 ) \ )
Phép quay
- Trong mặt phẳng cho điểm \ ( O \ ) và góc lượng giác \ ( \ alpha \ ). Phép biến hình biến điểm \ ( O \ ) thành chính nó, biến mỗi điểm \ ( M \ neq O \ ) thành điểm \ ( M ’ \ ) sao cho \ ( \ left \ { \ begin { matrix } OM = OM ’ \ \ ( OM, OM ’ ) = \ alpha \ end { matrix } \ right. \ ) được gọi là phép quay tâm \ ( O \ ), góc quay \ ( \ alpha \ )
- Kí hiệu \ ( Q_ { ( O ; \ alpha ) } \ )
***Chú ý : Trong trường hợp \( \alpha = 180^{\circ} \), khi đó \( O \) chính là trung điểm \( MM’ \) và phép quay \(Q_{(O;\alpha)}\) được gọi là phép đối xứng tâm \( O \). Kí hiệu \( D_O \). Nói cách khác : Phép đối xứng tâm là một trường hợp đặc biệt của phép quay
- Biểu thức tọa độ :
Trong mặt phẳng tọa độ \ ( Oxy \ ) cho \ ( I ( a ; b ) ; M ( x ; y ) ; M ’ ( x ’ ; y ’ ) \ ). Khi đó nếu \ ( M ’ = D_ { I } ( M ) \ ) thì \ ( \ left \ { \ begin { matrix } x ’ = 2 a – x \ \ y ’ = 2 b – y \ end { matrix } \ right. \ )
Ví dụ:
Trong mặt phẳng cho góc nhọn \ ( \ widehat { xOy } \ ) và điểm \ ( A \ ) thuộc miền trong của góc. Xác định đường thẳng \ ( d \ ) đi qua \ ( A \ ) cắt \ ( Ox ; Oy \ ) lần lượt tại \ ( M, N \ ) sao cho \ ( A \ ) là trung điểm \ ( MN \ )
Cách giải:

Giả sử đã dựng được hai điểm \ ( M, N \ ) thỏa mãn nhu cầu bài toán
Khi đó ta có :
\ ( M = D_A ( N ) \ ). Gọi \ ( O’y ’ = D_A ( Oy ) \ )
Khi đó ta có :
\ ( \ left \ { \ begin { matrix } M \ in O’y ’ \ \ M \ in Ox \ end { matrix } \ right. \ )
Vậy từ đó ta có cách dựng như sau :
Dựng \ ( O’y ’ = D_A ( Oy ) \ ). Khi đó, gọi \ ( M \ ) là giao điểm của \ ( Ox \ ) và \ ( O’y ’ \ ) .
Lấy \ ( N = D_A ( M ) \ ). Vậy ta dựng được hai điểm \ ( M, N \ ) cần tìm .
Phép đồng dạng là gì?
Phép đồng dạng tỉ số \ ( k > 0 \ ) là phép biến hình biến hai điểm \ ( M, N \ ) thành \ ( M ’, N ’ \ ) thỏa mãn nhu cầu \ ( M’N ’ = k. MN \ )
Tính chất của phép đồng dạng:
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay biến hóa thứ tự giữa ba điểm đó .
- Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng có độ dài gấp \ ( k \ ) lần .
- Biến tam giác thành tam giác đồng dạng với tỉ số \ ( k \ ), biến góc thành góc bằng nó .
- Biến đường tròn thành đường tròn có đường kính gấp \ ( k \ ) lần .
Phép vị tự
Trong những phép đồng dạng thì ở đây tất cả chúng ta chỉ đề cập đến phép vị tự, một phép biến hình toán 11 thường gặp trong những bài toán nâng cao
- Trong mặt phẳng cho điểm \ ( O \ ) và tỉ số \ ( k \ neq 0 \ ). Khi đó phép biến hình biến mỗi điểm \ ( M \ ) thành điểm \ ( M ’ \ ) sao cho \ ( \ overrightarrow { OM ’ } = k. \ overrightarrow { OM } \ ) được gọi là phép vị tự tâm \ ( O \ ) tỉ số \ ( k \ )
- Kí hiệu \ ( V_ { ( O ; k ) } \ )
Tâm vị tự
Nếu có phép vị tự tâm \ ( O \ ) biến đường tròn này thành đường tròn kia thì \ ( O \ ) được gọi là tâm vị tự của hai đường tròn đó
Hai đường tròn bất kỳ luôn có hai tâm vị tự. Nếu phép vị tự có tỉ số dương thì \ ( O \ ) được gọi là tâm vị tự ngoài. Nếu phép vị tự có tỉ số âm thì \ ( O \ ) được gọi là tâm vị tự trong
- Tâm vị tự trong :
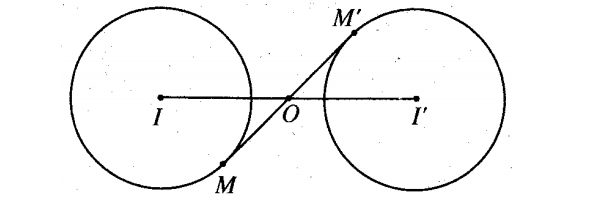
- Tâm vị tự ngoài :
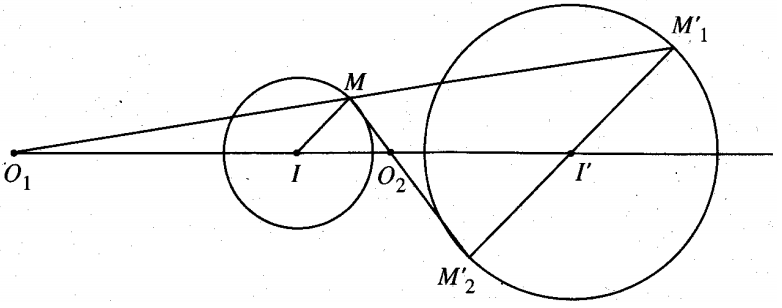
Ví dụ:
Cho đường tròn \ ( ( O ) \ ) với dây cung \ ( PQ \ ). Hãy dựng hình vuông \ ( ABCD \ ) có hai đỉnh \ ( A, B \ ) nằm trên đường thẳng \ ( PQ \ ) và hai đỉnh \ ( C, D \ ) nằm trên đường tròn .
Cách giải:

Giả sử đã dựng được hình vuông vắn \ ( ABCD \ ) thoả mãn điều kiện kèm theo của bài toán .
Dựng hình vuông \( PQMN \)
Gọi \ ( I \ ) là trung điểm của đoạn thẳng \ ( PQ \ Rightarrow OI \ ) là đường trung trực của \ ( PQ \ )
Vì \ ( \ left \ { \ begin { matrix } CD / / PQ \ \ OI \ bot PQ \ end { matrix } \ right. \ Rightarrow OI \ bot CD \ ) hay \ ( OI \ ) là trung trực của \ ( CD \ )
\ ( \ Rightarrow OI \ ) là trung trực của \ ( AB \ )
\ ( \ Rightarrow \ ) sống sót phép vị tự tâm \ ( I \ ) biến hình vuông \ ( PQMN \ ) thành hình vuông vắn \ ( ABCD \ )
Từ đó ta có cách dựng :
Dựng hình vuông \ ( PQMN \ ) .
Gọi \ ( C ; C ’ \ ) là giao của của đường thẳng \ ( IM \ ) và đường tròn \ ( ( O ) \ )
Gọi \ ( D ; D ’ \ ) là giao của của đường thẳng \ ( IN \ ) và đường tròn \ ( ( O ) \ ) ( sao cho \ ( C ; D \ ) nằm cùng phía so với \ ( PQ \ )
Gọi những điểm \ ( B, A, B ’, A ’ \ ) lần lượt là hình chiếu của những điểm \ ( C, D, C ’, D ’ \ ) trên đường thẳng \ ( PQ \ )
Ta được những hình vuông vắn \ ( ABCD \ ) và \ ( A’B ’ C’D ’ \ ) thoả mãn điều kiện kèm theo của bài toán .
Ứng dụng phép biến hình vào giải toán quỹ tích
Đối với mỗi bài toán khác nhau, ta lại sử dụng một phép biến hình khác nhau để tìm quỹ tích. Sau đây là giải pháp so với từng phép biến hình :
- Phép tịnh tiến
Chỉ ra được véc tơ \ ( \ vec { v } \ ) cố định và thắt chặt. Xét phép tịnh tiến \ ( T_ { \ vec { v } } \ ) biến điểm \ ( M \ ) thành điểm \ ( M ’ \ ). Biết điểm \ ( M \ ) chạy trên đường \ ( \ mathbb { C } \ ) thì quỹ tích điểm \ ( M ’ \ ) là đường \ ( \ mathbb { C } ’ \ ) thỏa mãn nhu cầu \ ( \ mathbb { C } ’ = T_ { \ vec { v } } ( \ mathbb { C } ) \ )
- Phép đối xứng trục
Chỉ ra được đường thẳng \ ( d \ ) cố định và thắt chặt. Xét phép đối xứng trục \ ( D_d \ ) biến điểm \ ( M \ ) thành điểm \ ( M ’ \ ). Biết điểm \ ( M \ ) chạy trên đường \ ( \ mathbb { C } \ ) thì quỹ tích điểm \ ( M ’ \ ) là đường \ ( \ mathbb { C } ’ \ ) thỏa mãn nhu cầu \ ( \ mathbb { C } ’ = D_d ( \ mathbb { C } ) \ )
- Phép quay
Chỉ ra được điểm \ ( O \ ) cố định và thắt chặt và một góc \ ( \ alpha \ ) không đổi. Xét phép quay \ ( Q_ { ( O ; \ alpha ) } \ ) biến điểm \ ( M \ ) thành điểm \ ( M ’ \ ). Biết điểm \ ( M \ ) chạy trên đường \ ( \ mathbb { C } \ ) thì quỹ tích điểm \ ( M ’ \ ) là đường \ ( \ mathbb { C } ’ \ ) thỏa mãn nhu cầu \ ( \ mathbb { C } ’ = Q_ { ( O ; \ alpha ) } ( \ mathbb { C } ) \ )
Phép đối xứng tâm là một trường hợp đặc biệt quan trọng của phép quay với \ ( \ alpha = \ pi \ )
- Phép vị tự
Chỉ ra được điểm \ ( O \ ) cố định và thắt chặt và tỉ số \ ( k \ ) không đổi. Xét phép vị tự \ ( V_ { ( O ; k ) } \ ) biến điểm \ ( M \ ) thành điểm \ ( M ’ \ ). Biết điểm \ ( M \ ) chạy trên đường \ ( \ mathbb { C } \ ) thì quỹ tích điểm \ ( M ’ \ ) là đường \ ( \ mathbb { C } ’ \ ) thỏa mãn nhu cầu \ ( \ mathbb { C } ’ = V_ { ( O ; k ) } ( \ mathbb { C } ) \ )
Ví dụ:
Cho đường tròn \ ( ( O ) \ ) và một điểm \ ( P \ ) nằm trong đường tròn đó. Một đường thẳng đổi khác đi qua \ ( P \ ) cắt đường tròn \ ( ( O ) \ ) tại hai điểm \ ( A ; B \ ). Tìm quỹ tích điểm \ ( M \ ) thỏa mãn nhu cầu đặc thù :
\ ( \ overrightarrow { PM } = \ overrightarrow { PA } + \ overrightarrow { PB } \ )
Cách giải:
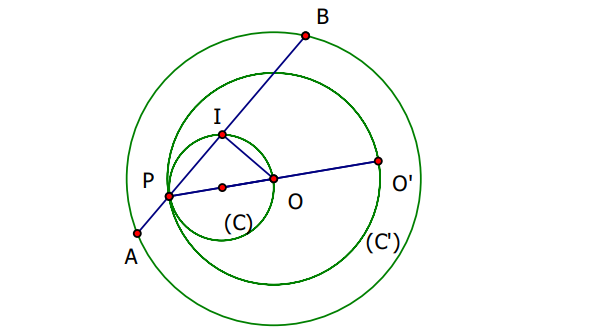
Gọi \ ( I \ ) là trung điểm \ ( AB \ ). Khi đó ta có :
\ ( \ left \ { \ begin { matrix } \ overrightarrow { PI } = \ overrightarrow { PA } + \ overrightarrow { AI } \ \ \ overrightarrow { PI } = \ overrightarrow { PB } + \ overrightarrow { BI } \ end { matrix } \ right. \ Rightarrow \ overrightarrow { PI } = \ frac { \ overrightarrow { PA } + \ overrightarrow { PB } + \ overrightarrow { AI } + \ overrightarrow { BI } } { 2 } = \ frac { \ overrightarrow { PA } + \ overrightarrow { PB } } { 2 } \ )
Do đó : \ ( \ overrightarrow { PM } = \ overrightarrow { PA } + \ overrightarrow { PB } = 2 \ overrightarrow { PI } \ )
Xét phép vị tự \ ( V_ { ( P ; 2 ) } \ ). Khi đó \ ( M = V_ { ( P ; 2 ) } ( I ) \ ; \ ; \ ; \ ; \ ; \ ; ( 1 ) \ )
Vì \ ( I \ ) là trung điểm \ ( AB \ ) nên \ ( \ Rightarrow OI \ bot AB \ Rightarrow OI \ bot PI \ Rightarrow \ ) quỹ tích điểm \ ( I \ ) là đường tròn đường kính \ ( PO \ ; \ ; \ ; \ ; \ ; \ ; \ ; ( 2 ) \ )
Từ \ ( ( 1 ) ( 2 ) \ Rightarrow \ ) quỹ tích điểm \ ( M \ ) là ảnh của đường tròn đường kính \ ( PO \ ) qua phép vị tự \ ( V_ { ( P ; 2 ) } \ )
Gọi \ ( O ’ \ ) là điểm đối xứng với \ ( P \ ) qua \ ( O \ )
Khi đó ta có :
\ ( V_ { ( P ; 2 ) } ( PO ) = PO ’ \ )
\ ( \ Rightarrow \ ) đường tròn đường kính \ ( PO ’ \ ) là ảnh của của đường tròn đường kính \ ( PO \ ) qua phép vị tự \ ( V_ { ( P ; 2 ) } \ )
Mà đường tròn đường kính \ ( PO ’ \ ) lại chính là đường tròn tâm \ ( O \ ) nửa đường kính \ ( OP \ )
Vậy quỹ tích điểm \ ( M \ ) cần tìm là đường tròn tâm \ ( O \ ) nửa đường kính \ ( OP \ )
Sơ đồ tư duy phép biến hình lớp 11
Sau đây là sơ đồ tư duy về những phép biến hình lớp 11 để những bạn hoàn toàn có thể dễ tổng hợp và ghi nhớ :

Các dạng bài tập phép biến hình lớp 11





Một số dạng trắc nghiệm phép biến hình
Sau đây là một bài bài tập trắc nghiệm phép biến hình giúp những bạn rèn luyện
Bài 1:
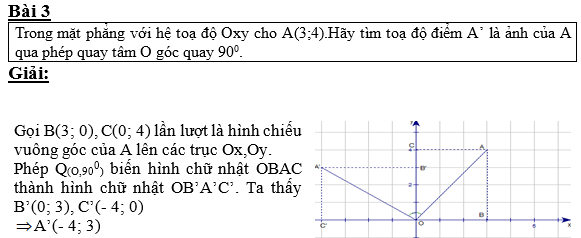
Trong mặt phẳng \ ( Oxy \ ) cho điểm \ ( A ( 3 ; 4 ) \ ). Tìm tọa độ điểm \ ( A ’ \ ) là ảnh của \ ( A \ ) qua phép quay \ ( Q_ { ( O ; \ frac { \ pi } { 2 } ) } \ )
- \ ( A ’ ( – 4 ; 3 ) \ )
- \ ( A ’ ( 4 ; 3 ) \ )
- \ ( A ’ ( – 4 ; – 3 ) \ )
- \ ( A ’ ( 4 ; – 3 ) \ )
Đáp án \( 1 \)
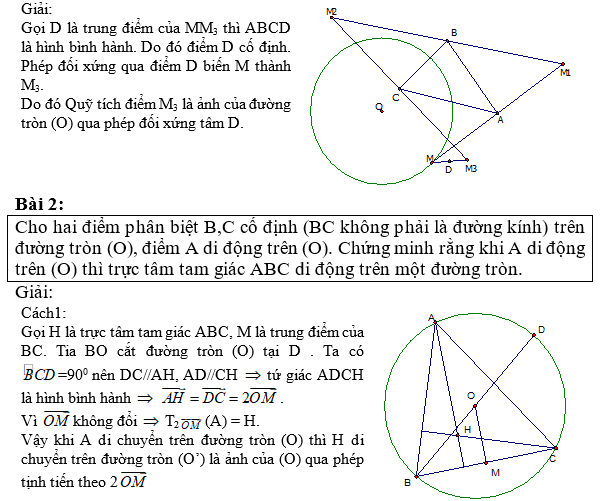
Bài 2:
Trong mặt phẳng \ ( Oxy \ ) cho đường tròn \ ( ( C ) \ ) có phương trình \ ( ( x-1 ) ^ 2 + ( y-2 ) ^ 2 = 4 \ ). Khi đó phép vị tự tâm \ ( O \ ) tỉ số \ ( k = – 2 \ ) biến đường tròn \ ( ( C ) \ ) thành đường tròn nào sau đây :
- \ ( ( x-2 ) ^ 2 + ( y-4 ) ^ 2 = 4 \ )
- \ ( ( x + 2 ) ^ 2 + ( y + 4 ) ^ 2 = 4 \ )
- \ ( ( x-2 ) ^ 2 + ( y-4 ) ^ 2 = 16 \ )
- \ ( ( x + 2 ) ^ 2 + ( y + 4 ) ^ 2 = 16 \ )
Đáp án \( 4 \)
Câu 3:
Trong những mệnh đề sau mệnh đề nào đúng ?
- Đường tròn là hình có vô số trục đối xứng
- Hình vuông là hình có vô số trục đối xứng
- Một hình có hai đường tròn cùng nửa đường kính thì có vô số trục đối xứng
- Một hình gồm hai đường thẳng vuông góc thì có vô số trục đối xứng
Đáp án \( 1 \)
Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp kiến thức và các phương pháp giải bài tập về các phép biến hình. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chuyên đề các phép biến hình lớp 11. Chúc bạn luôn học tốt!.
Xem thêm >>> Định nghĩa hình lăng trụ đều là gì? Tính chất hình lăng trụ đều và Bài tập
5
/
5
(
1
bầu chọn
)
Please follow and like us :
![]()
![]()
Source: https://sangtaotrongtamtay.vn
Category: Khoa học

Để lại một bình luận