Giải sách bài tập Toán 9 trang 60 tập 2 bài 48, 49, 50- Giải SBT Toán lớp 9 tập 2
Giải sách bài tập Toán 9 trang 60 tập 2 bài 48, 49, 50 – Giải SBT Toán lớp 9 tập 2 : với sách giải toán lớp 9 học kỳ 2 này chúng tôi được sưu tầm và biên soạn những giải thuật trong sách bài tập toán lớp 9 hay, đúng nhất và dễ hiểu nhất. cùng với đó trong sách giải bài tập toán lớp 9 tập 1 này chúng tôi có soạn thảo thêm hình vẽ vừa đủ cho những em và những bậc cha mẹ tưởng tượng nội dung …
Giải sách bài tập Toán 9 trang 60 tập 2 bài 48, 49, 50- Giải SBT Toán lớp 9 tập 2: với sách giải toán lớp 9 học kỳ 2 này chúng tôi được sưu tầm và biên soạn những lời giải trong sách bài tập toán lớp 9 hay, đúng nhất và dễ hiểu nhất. cùng với đó trong sách giải bài tập toán lớp 9 tập 1 này chúng tôi có soạn thảo thêm hình vẽ đầy đủ cho các em và các bậc phụ huynh hình dung nội dung cách giải dễ nhất. Cụ thể được qua bài viết Giải bài tập Toán 9 trang 60 tập 2 câu 48, 49, 50 dưới đây
Bạn đang đọc: Giải sách bài tập Toán 9 trang 60 tập 2 bài 48, 49, 50- Giải SBT Toán lớp 9 tập 2 – Sách giải các cấp : 1,2,3
Giải sách bài tập Toán 9 tập 1 trang 66
Giải sách bài tập Toán 8 tập 2 trang 83
# Giải sách bài tập Toán 9 trang 60 tập 2 bài 48, 49, 50

Giải bài tập Toán 9 trang 60 tập 2 câu 48, 49, 50
+ Bài tập Toán 9 trang 60
tập 2 câu 48
Giải những phương trình trùng phương
a. x4 – 8 × 2 – 9 = 0 b. y4 – 1,16 y2 + 0,16 = 0
c. z4 – 7 z2 – 144 = 0 d. 36 t4 – 13 t2 + 1 = 0

+ Bài tập Toán 9 trang 60
tập 2 câu 49
Chứng minh rằng khi a và c trái dấu thì phương trình trùng phương ax4 + bx2 + c = 0 chỉ có hai nghiệm và chúng là hai số đối nhau
+ Bài tập Toán 9 trang 60
tập 2 câu 50
Giải những phương trình sau bằng cách đặt ẩn số phụ
a. ( 4 x – 5 ) 2 – 6 ( 4 x – 5 ) + 8 = 0
b. ( x2 + 3 x – 1 ) 2 + 2 ( x2 + 3 x – 1 ) – 8 = 0
c. ( 2 × 2 + x – 2 ) 2 + 10 × 2 + 5 x – 16 = 0
d. ( x2 – 3 x + 4 ) ( x2 – 3 x + 2 ) = 3
#
Giải sách bài tập
toán
9 trang 60 tập 2 câu 48, 49, 50
+ Giải sách bài tập Toán 9 tập 2 trang 60 câu 48
a. Đặt m = x2. Điều kiện m ≥ 0
Ta có : x4 – 8 × 2 – 9 = 0 ⇔ mét vuông – 8 m – 9 = 0
Phương trìnhm2 – 8 m – 9 = 0 có thông số a = 1, b = – 8, c = – 9 nên có dạng a – b + c = 0
suy ra : m1 = – 1 ( loại ), mét vuông = – ( – 9 ) / 1 = 9
Ta có : x2 = 9 ⇒ x = ± 3
Vậy phương trình đã cho có 2 nghiệm : x1 = 3 ; x2 = – 3
b. Đặt m = y2. Điều kiện m ≥ 0
Ta có : y4 – 1,16 y2 + 0,16 = 0 ⇔ mét vuông – 1,16 m + 0,16 = 0
Phương trìnhm2 – 1,16 m + 0,16 = 0 có thông số a = 1, b = – 1,16, c = 0,16 nên có dạng a + b + c = 0
suy ra : m1 = 1, mét vuông = 0,16
Ta có : y2 = 1 ⇒ y = ± 1
y2 = 0,16 ⇒ y = ± 0,4
Vậy phương trình đã cho có 4 nghiệm : y1 = 1 ; y2 = – 1 ; y3 = 0,4 ; y4 = – 0,4
c. Đặt m = z2. Điều kiện m ≥ 0
Ta có : z4 – 7 z2 – 144 = 0 ⇔ mét vuông – 7 m – 144 = 0
Ta có : Δ = ( – 7 ) 2 – 4.1. ( – 144 ) = 49 + 576 = 625 > 0
√ Δ = √ 625 = 25

Ta có: z2 =16 ⇒ z=± 4
Vậy phương trình đã cho có 2 nghiệm : z1 = 4 ; z2 = – 4
d. Đặt m = t2. Điều kiện m ≥ 0
Ta có : 36 t4 – 13 t2 + 1 = 0 ⇔ 36 mét vuông – 13 m + 1 = 0
Ta có : Δ = ( – 13 ) 2 – 4.36.1 = 169 – 144 = 25 > 0
√ Δ = √ 25 = 5

Ta có: t2 =1/4 ⇒ t=± 1/2
t2 = 1/9 ⇒ t = ± 1/3
Vậy phương trình đã cho có 4 nghiệm :
t1 = 50% ; t2 = – 50% ; t3 = 1/3 ; t4 = – 1/3
e. Đặt m = x2. Điều kiện m ≥ 0
Ta có : 1/3. ( x4 ) – 50%. ( x2 ) + 1/6 = 0 ⇔ 2 × 4 – 3 × 2 + 1 = 0 ⇔ 2 mét vuông – 3 m + 1 = 0
Phương trình 2 mét vuông – 3 m + 1 = 0 có thông số a = 2, b = – 3, c = 1 nên có dạng a + b + c = 0
suy ra : m1 = 1, mét vuông = 50%
Ta có : x2 = 1 ⇒ x = ± 1
x2 = 50% ⇒ x = ± √ 2/2
Vậy phương trình đã cho có 4 nghiệm :
x1 = 1 ; x2 = – 1 ; x3 = ( √ 2 ) / 2 ; x4 = – √ 2/2
f. Đặt m = x2. Điều kiện m ≥ 0
Ta có : √ 3 x4 – ( 2 – √ 3 ) x2 – 2 = 0 ⇔ √ 3 mét vuông – ( 2 – √ 3 ) m – 2 = 0
Phương trình √ 3 mét vuông – ( 2 – √ 3 ) m – 2 = 0 có thông số a = √ 3, b = – ( 2 – √ 3 ), c = – 2 nên có dạng a – b + c = 0

+ Giải sách bài tập Toán 9 tập 2 trang 60 câu 49
Đặt m = x2. Điều kiện m ≥ 0
Ta có : ax4 + bx2 + c = 0 ⇔ am2 + bm + c = 0
Vì a và c trái dấu nên a / c < 0. Phương trình có 2 nghiệm phân biệt là m1 và mét vuông
Theo hệ thức Vi-ét, ta có : m1m2 = c / a
Vì a và c trái dấu nên c / a < 0 suy ra m1m2 < 0 hay m1 và mét vuông trái dấu nhau
Vì m1 và mét vuông trái dấu nhau nên có 1 nghiệm bị loại, giả sử loại m1
Khi đó x2 = mét vuông => x = ± √ mét vuông
Vậy phương trình trùng phương ax4 + bx2 + c = 0 chỉ có hai nghiệm và chúng là hai số đối nhau khi a và c trái dấu
+ Giải sách bài tập Toán 9 tập 2 trang 60 câu 50
a ) Đặt m = 4 x – 5
Ta có : ( 4 x – 5 ) 2 – 6 ( 4 x – 5 ) + 8 = 0 ⇔ mét vuông – 6 m + 8 = 0
Δ ’ = ( – 3 ) 2 – 1.8 = 9 – 8 = 1 > 0
√ Δ ’ = √ 1 = 1

Vậy phương trình đã cho có 2 nghiệm x1 =9/4 ,x2 =7/4
b ) Đặt m = x2 + 3 x – 1
Ta có : ( x2 + 3 x – 1 ) 2 + 2 ( x2 + 3 x – 1 ) – 8 = 0 ⇔ mét vuông + 2 m – 8 = 0
Δ ’ = 12 – 1. ( – 8 ) = 1 + 8 = 9 > 0
√ Δ ’ = √ 9 = 3

Với m = 2 thì : x2 + 3 x – 1 = 2 ⇔ x2 + 3 x – 3 = 0
Δ ’ = 32 – 4.1. ( – 3 ) = 9 + 12 = 21 > 0
√ Δ = √ 21

Với m = – 4 ta có : x2 + 3 x – 1 = – 4 ⇔ x2 + 3 x + 3 = 0
Δ = 32 – 4.1.3 = 9 – 12 = – 3 < 0
Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :

c ) Đặt m = 2 × 2 + x – 2
Ta có : ( 2 × 2 + x – 2 ) 2 + 10 × 2 + 5 x – 16 = 0
⇔ ( 2 × 2 + x – 2 ) 2 + 5 ( 2 × 2 + x – 2 ) – 6 = 0
⇔ mét vuông + 5 m – 6 = 0
Phương trình mét vuông + 5 m – 6 = 0 có thông số a = 1, b = 5, c = – 6 nên có dạng
a + b + c = 0
Suy ra : m1 = 1, mét vuông = – 6
m1 = 1 ta có : 2 × 2 + x – 2 = 1 ⇔ 2 × 2 + x – 3 = 0
Phương trình 2 × 2 + x – 3 = 0 có thông số a = 2, b = 1, c = – 3 nên có dạng
a + b + c = 0
Suy ra : x1 = 1, x2 = – 3/2
Với m = – 6 ta có : 2 × 2 + x – 2 = – 6 ⇔ 2 × 2 + x + 4 = 0
Δ = 12 – 4.2.4 = 1 – 32 = – 31 < 0. Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm : x1 = 1, x2 = - 32
d ) Đặt m = x2 - 3 x + 2
Ta có : ( x2 - 3 x + 4 ) ( x2 - 3 x + 2 ) = 3
⇔ [ ( x2 - 3 x + 2 + 2 ) ( x2 - 3 x + 2 ) - 3 = 0
⇔ ( x2 - 3 x + 2 ) 2 + 2 ( x2 - 3 x + 2 ) - 3 = 0
⇔ mét vuông + 2 m - 3 = 0
Phương trình mét vuông + 2 m - 3 = 0 có thông số a = 1, b = 2, c = - 3 nên có dạng
a + b + c = 0
suy ra : m1 = 1, mét vuông = - 3
Với m1 = 1 ta có : x2 - 3 x + 2 = 1 ⇔ x2 - 3 x + 1 = 0
Δ = ( - 3 ) 2 - 4.1.1 = 9 - 4 = 5 > 0
√ Δ = √ 5

e. Đặt m = x / ( x + 1 ). Điều kiện : x ≠ – 1
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9
⇔ 2 mét vuông – 5 m + 3 = 0
Phương trình 2 mét vuông – 5 m + 3 = 0 có thông số a = 2, b = – 5, c = 3 nên có dạng
a + b + c = 0
suy ra : m1 = 1, mét vuông = 3/2
Với m1 = 1 ta có : x / ( x + 1 ) = 1 ⇔ x = x + 1 ⇔ 0 x = 1 ( vô nghiệm )
Với m = 3/2 ta có : x / ( x + 1 ) = 3/2 ⇔ 2 x = 3 ( x + 1 )
⇔ 2 x = 3 x + 3 ⇔ x = – 3
Giá trị của x thỏa mãn nhu cầu điều kiện kèm theo bài toán
Vậy phương trình đã cho có 1 nghiệm : x = – 3
f. Đặt m = √ ( x – 1 ). Điều kiện : m ≥ 0, x ≥ 1
Ta có : x – √ ( x – 1 ) – 3 = 0 ⇔ ( x – 1 ) – √ ( x – 1 ) – 2 = 0
⇔ mét vuông – m – 2 = 0
Phương trình mét vuông – m – 2 = 0 có thông số a = 1, b = – 1, c = – 2 nên có dạng
a – b + c = 0
Suy ra : m1 = – 1 ( loại ), mét vuông = – ( – 2 ) / 1 = 2
Với m = 2 ta có : √ ( x – 1 ) = 2 ⇒ x – 1 = 4 ⇔ x = 5
Giá trị của x thỏa mãn nhu cầu điều kiện kèm theo bài toán
Vậy phương trình đã cho có 1 nghiệm : x = 5
# Cách sử dụng sách giải Toán 9 học kỳ 2 hiệu quả cho con
 Cách sử dụng sách giải Toán 9 học kỳ 2 hiệu quả cho con
Cách sử dụng sách giải Toán 9 học kỳ 2 hiệu quả cho con
+ Dành thời gian hướng dẫn con cách tham khảo sách như thế nào chứ không phải mua sách về và để con tự đọc. Nếu để con tự học với sách tham khảo rất dễ phản tác dụng.
+ Sách tham khảo rất đa dạng, có loại chỉ gợi ý, có loại giải chi tiết, có sách kết hợp cả hai. Dù là sách gợi ý hay sách giải thì mỗi loại đều có giá trị riêng. Theo sachgiai.net phụ huynh có vai trò giám sát định hướng cho con trong trường hợp nào thì dùng bài gợi ý, trường hợp nào thì đọc bài giải.
Ví dụ : Trước khi cho con đọc bài văn mẫu thì nên để con đọc bài gợi ý, tự làm bài ; sau đó đọc văn mẫu để bổ trợ thêm những ý thiếu vắng và học cách diễn đạt, cách sử dụng câu, từ .
+ Trong môn Văn nếu quá phụ thuộc vào các cuốn giải văn mẫu, đọc để thuộc lòng và vận dụng máy móc vào các bài tập làm văn thì rất nguy hiểm.
Phụ huynh chỉ nên mua những cuốn sách gợi ý cách làm bài chứ không nên mua sách văn mẫu, vì nó dễ khiến học viên bắt chước, làm triệt tiêu đi tư duy phát minh sáng tạo và mất dần cảm hứng. Chỉ nên cho học viên đọc những bài văn mẫu để học hỏi chứ tuyệt đối không khuyến khích con sử dụng cho bài văn của mình .
+ Trong môn Toán nếu con có lực học khá, giỏi thì nên mua sách giải sẵn các bài toán từ sách giáo khoa hoặc toán nâng cao để con tự đọc, tìm hiểu. Sau đó nói con trình bày lại. Quan trọng nhất là phải hiểu chứ không phải thuộc.
Nếu học viên trung bình, yếu thì phải có người giảng giải, kèm cặp thêm. Những sách trình diễn nhiều cách giải cho một bài toán thì chỉ tương thích với học viên khá giỏi .
Tags : bài tập toán lớp 9 học kỳ 2, vở bài tập toán lớp 9 tập 2, toán lớp 9 nâng cao, giải toán lớp 9, bài tập toán lớp 9, sách toán lớp 9, học toán lớp 9 không lấy phí, giải sbt toán 9, giải sbt toán 9 tập 2, giải toán 9 trang 60
Có thể bạn quan tâm
Source: https://sangtaotrongtamtay.vn
Category: Giáo dục
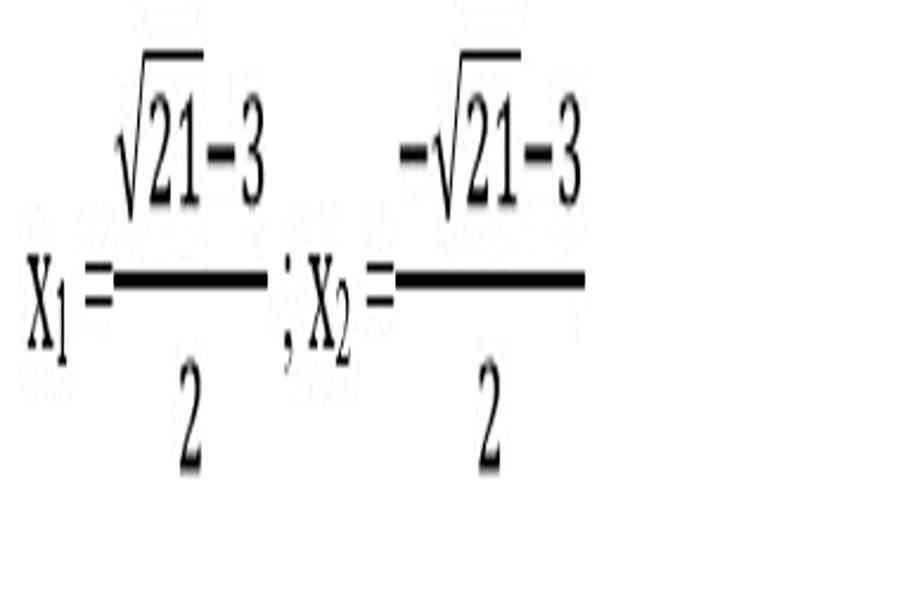
Để lại một bình luận