Đề cương lý thuyết học kì I môn toán lớp 10>

Lựa chọn câu để xem giải thuật nhanh hơn

Phần 1

Mệnh đề – Tập hợp

1. Mệnh đề

– Mệnh đề là những khẳng định có tính đúng(Đ) hoặc sai(S).

Mỗi mệnh đề phải đúng hoặc sai. Một mệnh đề không hề vừa đúng vừa sai .

– Phủ định của một mệnh đề \(A\) là mệnh đề \(\overline A \).

+ \ ( \ overline A \ ) đúng nếu \ ( A \ ) sai .
+ \ ( \ overline A \ ) sai nếu \ ( A \ ) đúng .

– Mệnh đề kéo theo: Mệnh đề kéo theo \(A \Rightarrow B\) chỉ sai khi \(A\) đúng,\(B\) sai

+ \ ( B \ Rightarrow A \ ) là mệnh đề hòn đảo của \ ( A \ Rightarrow B \ ) .
+ Nếu \ ( A \ Rightarrow B \ ) đúng thì \ ( A \ ) là điều kiện kèm theo đủ để có \ ( B \ ) và \ ( B \ ) là điều kiện kèm theo cần để có \ ( A \ ) .

– Mệnh đề tương đương:

+ Mệnh đề tương tự \ ( A \ Leftrightarrow B \ ) là một mệnh đề đúng nếu \ ( A \ ) và \ ( B \ ) cùng đúng hoặc cùng sai .
+ Nếu \ ( A \ Leftrightarrow B \ ) đúng thì :

• \(A \Rightarrow B\) là định lí thuận
• \(B \Rightarrow A\) là định lí đảo
• \(A \Leftrightarrow B\) là định lí thuận đảo
• \(A\) là điều kiện cần và đủ để có \(B\)
• \(B\) là điều kiện cần và đủ để có \(A\)

– Mệnh đề chứa biến, kí hiệu p(x)

• Mệnh đề chứa biến p(x) là một phát biểu có liên quan đến đại lượng thay đổi x.
• p(x) là một mệnh đề nếu ta cho x một giá trị nhất định.

–  Mệnh đề với mọi: \(\forall x \in X:p(x)\)

–  Mệnh đề tồn tại: \(\exists x \in X:p(x)\)

– Phương pháp chứng minh bằng phản chứng: Để chứng minh P đúng, ta giả sử P sai rồi sử dụng lập luận toán học để suy ra mâu thuẫn.

Các dạng toán thường gặp

1. Dạng 1: Định giá trị của một mệnh đề

Phương pháp

– Kiểm tra tính đúng sai của mệnh đề .
– Mệnh đề chứa biến : Tìm tập hợp \ ( D \ ) của những biến \ ( x \ ) để \ ( p ( x ) \ ) đúng hoặc sai .

2. Dạng 2: Phát biểu định lí dưới dạng điều kiện cần, đủ

Phương pháp

Nếu \ ( A \ Rightarrow B \ ) đúng : \ ( A \ ) là điều kiện kèm theo đủ để có \ ( B \ )
Nếu \ ( B \ Rightarrow A \ ) sai : \ ( B \ ) là điều kiện kèm theo cần để có \ ( A \ )
Nếu \ ( A \ Rightarrow B \ ) đúng và \ ( B \ Rightarrow A \ ) đúng : \ ( A \ ) là điều kiện kèm theo cần và đủ để có \ ( B \ ) .

3. Dạng 3: Tìm mệnh đề phủ định

Phương pháp

1 ) \ ( \ overline { A \ wedge B } \ Leftrightarrow \ overline A \ vee \ overline B \ )
\ ( \ overline { A \ vee B } \ Leftrightarrow \ overline A \ wedge \ overline B \ )
2 ) \ ( \ overline { \ forall x \ in D : p ( x ) } \ Leftrightarrow \ exists x \ in D : \ overline { p ( x ) } \ )
\ ( \ overline { \ exists x \ in D : p ( x ) } \ Leftrightarrow \ forall x \ in D : \ overline { p ( x ) } \ )

4. Dạng 4: Chứng minh định lí \(A \Rightarrow B\)

Phương pháp:

Cách 1: Chứng minh trực tiếp

Ta giả thiết A đúng, sử dụng giả thiết và suy luận toán học để dẫn đến B đúng.

Cách 2: Chứng minh bằng phản chứng

Ta giả thiết B sai, sử dụng suy luận toán học để dẫn đến A sai.

2.Tập hợp và các phép toán trên các tập hợp

Tập con : \ ( A \ subset B \ Leftrightarrow \ forall x, x \ in A \ Rightarrow x \ in B \ ) .
Hai tập hợp bằng nhau : \ ( A = B \ Leftrightarrow A \ subset B \ ) và \ ( B \ subset A \ ) .
Hợp của hai tập hợp : \ ( A \ cup B = { \ rm { \ { } } x \ left | { x \ in A } \ right. \ ) hoặc \ ( x \ in B { \ rm { \ } } } \ ) .
Giao của hai tập hợp : \ ( A \ cap B = { \ rm { \ { } } x \ left | { x \ in A } \ right. \ ) và \ ( x \ in B { \ rm { \ } } } \ ) .
Hiệu của 2 tập hợp bất kỳ : \ ( A \ backslash B = \ left \ { { x \ left | { x \ in A, x \ notin B } \ right. } \ right \ } \ ) .
Phép lấy phần bù của \ ( A \ ) trong \ ( E \ ) ( \ ( A \ subset E \ ) ) : \ ( { C_E } A = \ left \ { { x \ left | { x \ in E, x \ notin A } \ right. } \ right \ } \ ) .

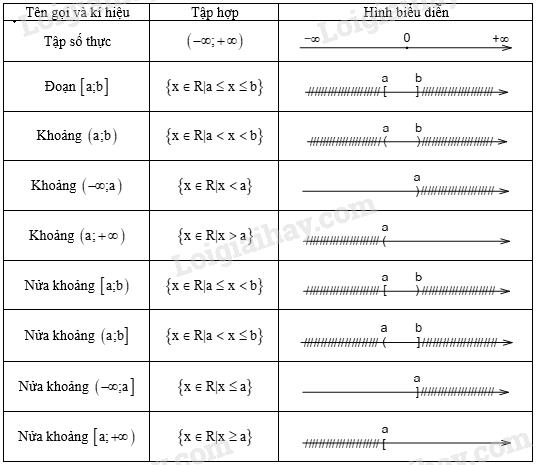
* Các tập hợp con của tập hợp số thực

\ ( \ mathbb { N } * \ subset \ mathbb { N } \ subset \ mathbb { Z } \ subset \ mathbb { Q } \ subset \ mathbb { R } \ )

 

Các dạng toán thường gặp

1. Dạng 1: Tìm tập hợp

Phương pháp

Phép liệt kê : \ ( A = \ left ( { { a_1 } ; { a_2 } ; { a_3 } ; … } \ right ) \ )
Nêu tính đặc trưng : \ ( A = \ left \ { { x \ in X | p ( x ) } \ right \ } \ )

2. Dạng 2: Tìm tập hợp con

Phương pháp

\ ( \ begin { array } { l } A \ subset B \ Leftrightarrow \ forall x \ in A \ Rightarrow x \ in B \ \ A \ not \ subset B \ Leftrightarrow \ exists x \ in A \ Rightarrow x \ notin B \ end { array } \ )

3. Dạng 3: Hai tập hợp bằng nhau

Phương pháp

\ ( A = B \ Leftrightarrow A \ subset B \ ) và \ ( B \ subset A \ )
\ ( A \ ne B \ Leftrightarrow A \ not \ subset B \ ) hoặc \ ( B \ not \ subset A \ )

4. Dạng 4: Các phép toán giao, hợp, hiệu

Phương pháp

B1 : Liệt kê A, B
B2 : \ ( A \ cap B \ ) : Lấy thành phần chung
\ ( A \ cup B \ ) : Lấy thành phần chung và riêng ( Chỉ ghi một lần những thành phần giống nhau )
\ ( A \ backslash B \ ) : Lấy thành phần của A và không phải của B

Phần 2

Hàm số bậc nhất và bậc hai

1. Tập xác định của hàm số

Tập xác lập của hàm số \ ( y = f \ left ( x \ right ) \ ) là tập hợp toàn bộ những số thực \ ( x \ ) sao cho biểu thức \ ( f \ left ( x \ right ) \ ) có nghĩa .
Điều kiện xác lập của một số ít dạng biểu thức :
\ ( \ dfrac { 1 } { A } \ ) có nghĩa khi và chỉ khi \ ( A \ ne 0 \ )
\ ( \ sqrt A \ ) có nghĩa khi và chỉ khi \ ( A \ ge 0 \ )
\ ( \ dfrac { 1 } { { \ sqrt A } } \ ) có nghĩa khi và chỉ khi \ ( A > 0 \ )

2. Tính chẵn – lẻ của hàm số

Cho hàm số \ ( y = f \ left ( x \ right ) \ ) xác lập trên \ ( D \ )
a ) Hàm số \ ( f \ ) là hàm số chẵn nếu thỏa mãn nhu cầu cả 2 điều kiện kèm theo :
\ ( \ left \ { \ begin { array } { l } – x \ in D \ \ f \ left ( { – x } \ right ) = f \ left ( x \ right ) \ end { array } \ right. \ forall x \ in D \ )

Đồ thị của \(f\) nhận trục tung làm trục đối xứng.

b ) Hàm số \ ( f \ ) là hàm số lẻ nếu thỏa mãn nhu cầu cả 2 điều kiện kèm theo :
\ ( \ left \ { \ begin { array } { l } – x \ in D \ \ f \ left ( { – x } \ right ) = – f \ left ( x \ right ) \ end { array } \ right. \ forall x \ in D \ )

Đồ thị của \(f\) nhận gốc tọa độ  làm tâm đối xứng.

3. Sự biến thiên

Hàm số \ ( y = f \ left ( x \ right ) \ ) xác lập trên \ ( D \ )
Hàm số đồng biến trên \ ( D \ ) nếu \ ( \ forall { x_1 }, { x_2 } \ in D : { x_1 } < { x_2 } \ Rightarrow f \ left ( { { x_1 } } \ right ) < f \ left ( { { x_2 } } \ right ) \ ) . Hàm số nghịch biến trên \ ( D \ ) nếu \ ( \ forall { x_1 }, { x_2 } \ in D : { x_1 } < { x_2 } \ Rightarrow f \ left ( { { x_1 } } \ right ) > f \ left ( { { x_2 } } \ right ) \ ) .

4. Tịnh tiến đồ thị hàm số

Trong \ ( { \ rm { Oxy } } \ ), cho đồ thị \ ( \ left ( G \ right ) \ ) của hàm số \ ( y = f \ left ( x \ right ) \ ) ; \ ( p \ ) và \ ( q \ ) là hai số dương tùy ý. Khi đó :
a ) Tịnh tiến \ ( \ left ( G \ right ) \ ) lên trên \ ( q \ ) đơn vị chức năng thì được đồ thị hàm số \ ( y = f \ left ( x \ right ) + q \ )
b ) Tịnh tiến \ ( \ left ( G \ right ) \ ) xuống dưới \ ( q \ ) đơn vị chức năng thì được đồ thị hàm số \ ( y = f \ left ( x \ right ) – q \ )
c ) Tịnh tiến \ ( \ left ( G \ right ) \ ) sang trái \ ( p \ ) đơn vị chức năng thì được đồ thị hàm số \ ( y = f \ left ( { x + p } \ right ) \ )
d ) Tịnh tiến \ ( \ left ( G \ right ) \ ) sang phải \ ( p \ ) đơn vị chức năng thì được đồ thị hàm số \ ( y = f \ left ( { x – p } \ right ) \ )

5. Hàm số bậc nhất

a) Định nghĩa: Hàm số bậc nhất là hàm số có dạng \(y = ax + b\left( {a \ne 0} \right)\)

Tập xác lập : \ ( D = \ mathbb { R } \ ) .

b) Sự biến thiên (tính đơn điệu)

Khi \ ( a > 0 \ ), hàm số đồng biến trên \ ( \ mathbb { R } \ )
Khi \ ( a < 0 \ ), hàm số nghịch biến trên \ ( \ mathbb { R } \ ) Bảng biến thiên :

c) Đồ thị

Đặc điểm : Đồ thị của hàm số \ ( y = ax + b \ left ( { a \ ne 0 } \ right ) \ ) là một đường thẳng \ ( d \ ) có thông số góc a, không song song và không trùng với những trục tọa độ. Đồ thị cắt trục tung tại \ ( B \ left ( { 0 ; b } \ right ) \ ) và cắt trục hoành tại \ ( A \ left ( { – \ dfrac { b } { a } ; 0 } \ right ) \ ) .
Chú ý :
+ Hệ số góc \ ( a = \ tan \ alpha \ ) với \ ( \ alpha \ ) là góc tạo bởi \ ( d \ ) và \ ( Ox \ ) .
+ Hàm số \ ( y = b \ left ( { a = 0 } \ right ) \ ) là hàm hằng, đồ thì là đường thẳng song song \ ( \ left ( { b \ ne 0 } \ right ) \ ) hoặc trùng \ ( \ left ( { b = 0 } \ right ) \ ) với trục hoành .
+ Cho 2 đường thẳng \ ( \ left ( d \ right ) : y = ax + b \ ) và \ ( \ left ( { d ‘ } \ right ) : y = a’x + b ‘ \ ), ta có :

• \(\left( d \right)\) song song với \(\left( {d’} \right)\)\( \Leftrightarrow a = a’\) và \(b \ne b’\).
• \(\left( d \right)\) trùng với \(\left( {d’} \right)\)\( \Leftrightarrow a = a’\) và \(b = b’\).
• \(\left( d \right)\) cắt \(\left( {d’} \right)\)\( \Leftrightarrow a \ne a’\).
• \(\left( d \right)\) vuông góc với \(\left( {d’} \right)\)\( \Leftrightarrow a.a’ =  – 1\).

d) Hàm số bậc nhất trên từng khoảng

Hàm số bậc nhất trên từng khoảng chừng là sự “ lắp ghép ” của những hàm số bậc nhất khác nhau trên từng khoảng chừng. Hàm số có dạng :
\ ( y = \ left \ { \ begin { array } { l } { a_1 } x + { b_1 } { \ rm { } } x \ in { { \ rm { D } } _1 } \ \ { a_2 } x + { b_2 } { \ rm { } } x \ in { { \ rm { D } } _2 } \ \ … \ end { array } \ right. \ ) với \ ( { D_1 }, { D_2 } \ ) là những khoảng chừng ( đoạn, nửa khoảng chừng ) trên \ ( \ mathbb { R } \ )

Sự biến thiên:

Xét tính đồng biến, nghịch biến của những hàm số :
\ ( y = { a_1 } x + { b_1 } \ ) trên \ ( { D_1 } \ )
\ ( y = { a_2 } x + { b_2 } \ ) trên \ ( { D_2 } \ )
…
Từ đó suy ra sự biến thiên của hàm số đã cho trên \ ( { D_1 } \ cup { D_2 } \ cup … \ )
Đồ thị của hàm số này là đường tạo bởi việc lắp ghép đồ thị những hàm số
\ ( y = { a_1 } x + { b_1 } \ ) trên \ ( { D_1 } \ ), \ ( y = { a_2 } x + { b_2 } \ ) trên \ ( { D_2 } \ ) .

Hàm số \(y = \left| {ax + b} \right|\left( {a \ne 0} \right)\): Là hàm số bậc nhất trên từng khoảng

\ ( y = \ left \ { \ begin { array } { l } ax + b { \ rm { khi } } x \ ge – \ dfrac { b } { a } \ \ – ax – b { \ rm { khi } } x \ le – \ dfrac { b } { a } \ end { array } \ right. \ )
Cách vẽ đồ thị hàm số \ ( y = \ left | { ax + b } \ right | \ left ( { a \ ne 0 } \ right ) \ ) : Vẽ hai đường thẳng \ ( y = ax + b \ ) và \ ( y = – ax – b \ ) rồi xóa đi phần đường thẳng nằm dưới trục hoành .

6. Hàm số bậc hai

a) Định nghĩa: Hàm số bậc hai là hàm số có dạng \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\).

b) Sự biến thiên

– Nếu \ ( a > 0 \ ), hàm số đồng biến trên \ ( \ left ( { – \ dfrac { b } { { 2 a } } ; + \ infty } \ right ) \ ), nghịch biến trên \ ( \ left ( { – \ infty ; – \ dfrac { b } { { 2 a } } } \ right ) \ ). Giá trị nhỏ nhất của hàm số trên \ ( \ mathbb { R } \ ) là \ ( – \ dfrac { \ Delta } { { 4 a } } \ ) tại \ ( x = – \ dfrac { b } { { 2 a } } \ ) .
– Nếu \ ( a < 0 \ ), hàm số đồng biến trên \ ( \ left ( { - \ infty ; - \ dfrac { b } { { 2 a } } } \ right ) \ ), nghịch biến trên \ ( \ left ( { - \ dfrac { b } { { 2 a } } ; + \ infty } \ right ) \ ). Giá trị lớn nhất của hàm số trên \ ( \ mathbb { R } \ ) là \ ( - \ dfrac { \ Delta } { { 4 a } } \ ) tại \ ( x = - \ dfrac { b } { { 2 a } } \ ) .

c) Đồ thị

– Có dáng là đường Parabol có đỉnh \ ( \ left ( { – \ dfrac { b } { { 2 a } } ; – \ dfrac { \ Delta } { { 4 a } } } \ right ) \ ), \ ( \ Delta = { b ^ 2 } – 4 ac \ ) .
– Trục đối xứng là đường thẳng \ ( x = – \ dfrac { b } { { 2 a } } \ )
– Bề lõm hướng lên trên khi \ ( a > 0 \ ), hướng xuống dưới khi \ ( a < 0 \ ) .

–       Cách vẽ:

• Xác định đỉnh \(\left( { – \dfrac{b}{{2a}}; – \dfrac{\Delta }{{4a}}} \right)\) trên \(Oxy\).
• Vẽ trục đối xứng \(x =  – \dfrac{b}{{2a}}\).
• Tìm các điểm thuộc Parabol (thay lần lượt các giá trị của \(x\) vào \(y = a{x^2} + bx + c\) rồi tìm y để được các điểm \(\left( {x;y} \right)\) tương ứng)
• Dựa bề lõm và trục đối xứng, nối đỉnh với các điểm vừa tìm được với nhau.

Các dạng toán thường gặp

1. Dạng 1: Tìm tập xác định của hàm số

Phương pháp

Tập xác lập của hàm số \ ( y = f \ left ( x \ right ) \ ) là tập những giá trị của \ ( x \ ) sao cho biểu thức \ ( f \ left ( x \ right ) \ ) có nghĩa

Chú ý : Nếu \(P\left( x \right)\) là một đa thức thì:
*  \(\dfrac{1}{{P\left( x \right)}}\) có nghĩa\( \Leftrightarrow P\left( x \right) \ne 0\)                             

* \ ( \ sqrt { P \ left ( x \ right ) } \ ) có nghĩa \ ( \ Leftrightarrow P \ left ( x \ right ) \ ge 0 \ )
* \ ( \ dfrac { 1 } { { \ sqrt { P \ left ( x \ right ) } } } \ ) có nghĩa \ ( \ Leftrightarrow P \ left ( x \ right ) > 0 \ )

2. Dạng 2: Xét tính chẵn, lẻ của hàm số

Phương pháp:

Bước 1 : Tìm tập xác lập của hàm số .
Bước 2 : Kiểm tra
– Nếu \ ( \ forall x \ in D \ Rightarrow – x \ in D \ ) chuyển qua bước ba .
– Nếu \ ( \ exists { x_0 } \ in D \ Rightarrow – { x_0 } \ notin D \ ) Kết luận hàm không chẵn cũng không lẻ .
Bước 3 : Xác định \ ( f \ left ( { – x } \ right ) \ ) và so sánh với \ ( f \ left ( x \ right ) \ ) .
– Nếu bằng nhau thì Kết luận hàm số là chẵn
– Nếu đối nhau thì Tóm lại hàm số là lẻ
– Nếu sống sót một giá trị \ ( \ exists { x_0 } \ in D \ ) mà \ ( f \ left ( { – { x_0 } } \ right ) \ ne f \ left ( { { x_0 } } \ right ), f \ left ( { – { x_0 } } \ right ) \ ne – f \ left ( { { x_0 } } \ right ) \ ) Tóm lại hàm số không chẵn cũng không lẻ .

3.Dạng 3: Xét tính đơn điệu của hàm số

Phương pháp

Cách 1: Cho hàm số \(y = f\left( x \right)\) xác định trên \(K\). Lấy \({x_1},{x_2} \in K;{\rm{ }}{x_1} < {x_2}\), đặt \(T = f({x_2}) - f({x_1})\)

+ ) Hàm số đồng biến trên \ ( K \ Leftrightarrow T > 0 \ ) .
+ ) Hàm số nghịch biến trên \ ( K \ Leftrightarrow T < 0 \ ) .

Cách 2: Cho hàm số \(y = f\left( x \right)\) xác định trên \(K\). Lấy \({x_1},{x_2} \in K;{\rm{ }}{x_1} \ne {x_2}\), đặt \(T = \dfrac{{f({x_2}) – f({x_1})}}{{{x_2} – {x_1}}}\)

+ ) Hàm số đồng biến trên \ ( K \ Leftrightarrow T > 0 \ ) .
+ ) Hàm số nghịch biến trên \ ( K \ Leftrightarrow T < 0 \ ) .

4. Dạng  4: Đồ thị của hàm số và tịnh tiến đồ thị hàm số

Phương pháp:

Sử dụng định nghĩa điểm thuộc đồ thị hàm số và định lý về tịnh tiến đồ thị một hàm số .

5. Dạng 5: Xác định hàm số bậc hai.

Phương pháp

Hàm số bậc hai có dạng : \ ( y = a { x ^ 2 } + bx + c \ left ( { a \ ne 0 } \ right ) \ ). Đồ thị của hàm số là Parabol ( P. ) có :

• Hoành độ đỉnh \({x_0} =  – \dfrac{b}{{2a}}\)
• Trục đối xứng là đường thẳng \(\left( \Delta  \right):x =  – \dfrac{b}{{2a}}\)

6. Dạng 6: Tìm GTLN-GTNN nhờ Parabol

Phương pháp

Xét Parabol ( P. ) : \ ( y = a { x ^ 2 } + bx + c \ left ( { a > 0 } \ right ) \ ). Tìm \ ( \ mathop { \ max } \ limits_D y = GTLN ( y ) ; \ mathop { \ min } \ limits_D y = GTNN ( y ) \ ) với \ ( D = \ left [ { \ alpha ; \ beta } \ right ] \ )
Hoành độ đỉnh Parabol ( P. ) : \ ( { x_0 } = – \ dfrac { b } { { 2 a } } \ ) .
Nếu \ ( { x_0 } \ in D : \ left \ { \ begin { array } { l } GTLN ( y ) = \ max \ left \ { { f \ left ( \ alpha \ right ) ; f \ left ( \ beta \ right ) } \ right \ } \ \ GTNN ( y ) = f \ left ( { { x_0 } } \ right ) \ end { array } \ right. \ )
Nếu \ ( { x_0 } \ notin D : \ left \ { \ begin { array } { l } GTLN ( y ) = \ max \ left \ { { f \ left ( \ alpha \ right ) ; f \ left ( \ beta \ right ) } \ right \ } \ \ GTNN ( y ) = \ min \ left \ { { f \ left ( \ alpha \ right ) ; f \ left ( \ beta \ right ) } \ right \ } \ end { array } \ right. \ )

Phần 3

Phương trình – Hệ phương trình

1. Điều kiện xác định của phương trình

Cho hai hàm số \ ( y = f \ left ( x \ right ) \ ) và \ ( y = g \ left ( x \ right ) \ ) có tập xác lập lần lượt là \ ( { D_1 } \ ) và \ ( { D_2 } \ ) .
Khi đó phương trình \ ( f \ left ( x \ right ) = g \ left ( x \ right ) \ ) có điều kiện kèm theo xác lập là \ ( x \ in D = { D_1 } \ cap { D_2 } \ ) .
Các nghiệm của phương trình \ ( f \ left ( x \ right ) = g \ left ( x \ right ) \ ) là hoành độ những giao điểm của đồ thị hai hàm số \ ( y = f \ left ( x \ right ) \ ) và \ ( y = g \ left ( x \ right ) \ ) .

2. Phương trình tương đương; Phương trình hệ quả

2.1. Phương trình tương đương và phép biến đổi tương đương

Hai phương trình tương tự nếu chúng có cùng tập nghiệm .

Một số phép biến đổi tương đương:

1. Cho phương trình \ ( f \ left ( x \ right ) = g \ left ( x \ right ) \ ) có tập xác lập \ ( D \ ) và hàm số \ ( y = h \ left ( x \ right ) \ ) xác lập trên \ ( D \ ) ( TXĐ của \ ( h \ left ( x \ right ) \ ) hoàn toàn có thể là một tập chứa \ ( D \ ) ). Khi đó :

• \(f\left( x \right) = g\left( x \right) \Leftrightarrow f\left( x \right) + h\left( x \right) = g\left( x \right) + h\left( x \right)\)
• \(f\left( x \right) = g\left( x \right) \Leftrightarrow f\left( x \right)h\left( x \right) = g\left( x \right)h\left( x \right)\) nếu \(h\left( x \right) \ne 0\forall x \in D\).

1. Nếu \ ( f \ left ( x \ right ), g \ left ( x \ right ) \ ) cùng dấu thì : \ ( f \ left ( x \ right ) = g \ left ( x \ right ) \ Leftrightarrow { \ left [ { f \ left ( x \ right ) } \ right ] ^ 2 } = { \ left [ { g \ left ( x \ right ) } \ right ] ^ 2 } \ ) .

2.2. Phương trình hệ quả

Nếu mọi nghiệm của \ ( f \ left ( x \ right ) = g \ left ( x \ right ) \ ) đều là nghiệm của \ ( { f_1 } \ left ( x \ right ) = { g_1 } \ left ( x \ right ) \ ) thì \ ( { f_1 } \ left ( x \ right ) = { g_1 } \ left ( x \ right ) \ ) là phương trình hệ quả của \ ( f \ left ( x \ right ) = g \ left ( x \ right ) \ ). Ta viết :
\ ( f \ left ( x \ right ) = g \ left ( x \ right ) \ Rightarrow \ ) \ ( { f_1 } \ left ( x \ right ) = { g_1 } \ left ( x \ right ) \ ) .

Phép biến đổi dẫn đến phương trình hệ quả:

\ ( f \ left ( x \ right ) = g \ left ( x \ right ) \ Rightarrow { \ left [ { f \ left ( x \ right ) } \ right ] ^ 2 } = { \ left [ { g \ left ( x \ right ) } \ right ] ^ 2 } \ )

3. Phương trình bậc nhất; Phương trình bậc hai; Định lý Viéte

3.1. Giải và biện luận phương trình dạng \(ax + b = 0\)

1 ) \ ( a \ ne 0 \ ) : Phương trình có một nghiệm duy nhất \ ( x = – \ dfrac { b } { a } \ ) .
2 ) \ ( a = 0 \ ) và \ ( b \ ne 0 \ ) : Phương trình vô nghiệm .
3 ) \ ( a = b = 0 \ ) : Phương trình có vô số nghiệm .

3.2. Giải và biện luận nghiệm phương trình dạng \(a{x^2} + bx + c = 0\)

1 ) \ ( a = 0 \ ) : Phương trình trở về dạng \ ( ax + b = 0 \ )
2 ) \ ( a \ ne 0 \ ) :

• \(\Delta  > 0\): Phương trình có 2 nghiệm phân biệt

\ ( x = \ dfrac { { – b – \ sqrt \ Delta } } { { 2 a } } \ ) và \ ( x = \ dfrac { { – b + \ sqrt \ Delta } } { { 2 a } } \ )

• \(\Delta  = 0\): Phương trình có nghiệm kép \(x =  – \dfrac{b}{{2a}}\)
• \(\Delta  < 0\): Phương trình vô nghiệm.

3.3. Sử dụng định lý Viéet

Cho phương trình bậc hai \ ( a { x ^ 2 } + bx + c = 0 \ ) có 2 nghiệm \ ( { x_1 } \ le { x_2 } \ ). Đặt \ ( S = – \ dfrac { b } { a } ; P = \ dfrac { c } { a } \ ). Khi đó :
+ Nếu \ ( P < 0 \ ) thì \ ( { x_1 } < 0 < { x_2 } \ ) ( 2 nghiệm trái dấu ) . + Nếu \ ( P > 0 \ ) và \ ( S > 0 \ ) thì \ ( 0 < { x_1 } \ le { x_2 } \ ) ( 2 nghiệm dương ). ( Cần tính \ ( \ Delta \ ) trước ) . + Nếu \ ( P > 0 \ ) và \ ( S < 0 \ ) thì \ ( { x_1 } \ le { x_2 } < 0 \ ) ( 2 nghiệm âm ). ( Cần tính \ ( \ Delta \ ) trước ) .

4. Hệ phương trình

Hệ hai phương trình bậc nhất hai ẩn có dạng :
\ ( \ left \ { \ begin { array } { l } ax + by = c \ \ a’x + b’y = c ‘ \ end { array } \ right. ( I ) { \ rm { } } \ left ( { { a ^ 2 } + { b ^ 2 } \ ne 0 ; a { ‘ ^ 2 } + b { ‘ ^ 2 } \ ne 0 } \ right ) \ )
Gọi \ ( d, d ‘ \ ) lần lượt là những đường thẳng \ ( ax + by = c \ ) và \ ( a’x + b’y = c ‘ \ ). Khi đó :
Hệ ( I ) có nghiệm \ ( \ Leftrightarrow d \ ) và \ ( d ‘ \ ) cắt nhau .
Hệ ( I ) vô nghiệm \ ( \ Leftrightarrow d \ ) và \ ( d ‘ \ ) song song .
Hệ ( I ) vô số nghiệm \ ( \ Leftrightarrow d \ ) và \ ( d ‘ \ ) trùng nhau .

Các bước giải và biện luận hệ phương trình bậc nhất hai ẩn:

Bước 1 : Tính những giá trị \ ( D = ab ‘ – a’b ; { D_x } = cb ‘ – c’b ; { D_y } = ac ‘ – a’c \ )
Bước 2 : Biện luận
1. Nếu \ ( D \ ne 0 \ ) hệ có một nghiệm duy nhất \ ( \ left ( { x ; y } \ right ) = \ left ( { \ dfrac { { { D_x } } } { D } ; \ dfrac { { { D_y } } } { D } } \ right ) \ ) .
2. Nếu \ ( D = 0 \ ) và :

• \({D_x} \ne 0\) hoặc \({D_y} \ne 0\) thì hệ vô nghiệm.
• \({D_x} = {D_y} = 0\) thì hệ có vô số nghiệm. Tập nghiệm của hệ là tập nghiệm của phương trình \(ax + by = c\).

Nguyên tắc giải hệ phương trình nhiều ẩn : Khử bớt ẩn bằng chiêu thức thế hoặc cộng đại số như so với hệ phương trình hai ẩn .

Các dạng toán thường gặp

1. Dạng 1: Giải và biện luận nghiệm của phương trình \(ax + b = 0\)

Phương pháp 

Sử dụng định lí về giải và biện luận nghiệm phương trình bậc nhất một ẩn .

2. Dạng 2: Tìm m để phương trình thỏa mãn điều kiện cho trước

Phương pháp

Sử dụng các định lí về nghiệm của phương trình  để biện luận

3. Dạng 3: Giải và biện luận nghiệm phương trình \(a{x^2} + bx + c = 0\)

4. Dạng 4: Phương trình chứa ẩn trong dấu giá trị tuyệt đối

Phương pháp

Xét các khoảng rồi bỏ dấu giá trị tuyệt đối

5. Dạng 5: Phương trình chứa ẩn ở mẫu – Phương trình bậc cao

Phương pháp

Đưa về phương trình đơn giản hơn (phương trình tích, phương trình bậc nhất và bậc hai, phương trình trùng phương,…) để giải.

6. Dạng 6: Phương trình vô tỷ (chứa căn thức)

+ ) \ ( \ sqrt { f \ left ( x \ right ) } = g \ left ( x \ right ) \ Leftrightarrow \ left \ { \ begin { array } { l } g \ left ( x \ right ) \ ge 0 \ \ f \ left ( x \ right ) = { g ^ 2 } \ left ( x \ right ) \ end { array } \ right. \ )
+ ) \ ( \ sqrt { f \ left ( x \ right ) } = \ sqrt { g \ left ( x \ right ) } \ Leftrightarrow \ left \ { \ begin { array } { l } f \ left ( x \ right ) \ ge 0 \ \ f \ left ( x \ right ) = g \ left ( x \ right ) \ end { array } \ right. \ ) hoặc \ ( \ left \ { \ begin { array } { l } g \ left ( x \ right ) \ ge 0 \ \ f \ left ( x \ right ) = g \ left ( x \ right ) \ end { array } \ right. \ )
ở đây, với những bài toán đơn cử những em hoàn toàn có thể chọn một trong hai điều kiện kèm theo \ ( f \ left ( x \ right ) \ ge 0 \ ) hoặc \ ( g \ left ( x \ right ) \ ge 0 \ ) phụ thuộc vào vào hai hàm \ ( f \ left ( x \ right ), g \ left ( x \ right ) \ ), hàm nào đơn thuần hơn thì ta chọn, không cần giải hết những điều kiện kèm theo \ ( f \ left ( x \ right ) \ ge 0 \ ) và \ ( g \ left ( x \ right ) \ ge 0 \ ) .
+ ) \ ( f \ left ( x \ right ). \ sqrt { g \ left ( x \ right ) } = 0 \ Leftrightarrow \ left [ \ begin { array } { l } g \ left ( x \ right ) = 0 \ \ \ left \ { \ begin { array } { l } g \ left ( x \ right ) \ ge 0 \ \ f \ left ( x \ right ) = 0 \ end { array } \ right. \ end { array } \ right. \ ) .

7. Dạng 7: Hệ hai phương trình 2 ẩn

a. Hệ gồm một phương trình bậc nhất và một phương trình bậc hai

\( \bullet \)   Dạng tổng quát: \(\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\left( 1 \right)\\d{x^2} + exy + f{y^2} + gx + hy = i\,\,\,\,\,\left( 2 \right)\end{array} \right.\)                       

\( \bullet \)   Phương pháp giải:

– Bước 1 : Từ phương trình bậc nhất ( 1 ), rút \ ( x \ ) theo \ ( y \ ) ( hoặc \ ( y \ ) theo \ ( x \ ) ) .
– Bước 2 : Thế vào phương trình còn lại ( 2 ) để giải tìm \ ( x \ ) ( hoặc tìm \ ( y \ ) ) .

b. Hệ phương trình đối xứng loại I

\( \bullet \)   Dấu hiệu nhận dạng: Khi thay đổi vị trí \(x\) và \(y\) cho nhau thì hệ không thay đổi và trật tự các phương trình cũng không thay đổi.

\( \bullet \)   Phương pháp giải:

– Bước 1 : đặt \ ( S = x + y, { \ rm { } } P = xy. \ )
– Bước 2 : Giải hệ với ẩn \ ( S, { \ rm { } } P \ ) với điều kiện kèm theo có nghiệm \ ( ( x ; y ) \ ) là \ ( { S ^ 2 } \ ge 4P. \ )
– Bước 3 : Tìm nghiệm \ ( ( x ; y ) \ ) bằng cách thế vào phương trình \ ( { X ^ 2 } – SX + P. = 0. \ )

Chú ý:

Một số biến hóa để đưa về dạng tổng – tích thường gặp :
+ ) \ ( { x ^ 2 } + { y ^ 2 } = { ( x + y ) ^ 2 } – 2 xy = { S ^ 2 } – 2P. \ )
+ ) \ ( { x ^ 3 } + { y ^ 3 } = { ( x + y ) ^ 3 } – 3 xy ( x + y ) = { S ^ 3 } – 3SP. \ )
+ ) \ ( { ( x – y ) ^ 2 } = { ( x + y ) ^ 2 } – 4 xy = { S ^ 2 } – 4P. \ )
+ ) \ ( { x ^ 4 } + { y ^ 4 } = { ( { x ^ 2 } + { y ^ 2 } ) ^ 2 } – 2 { x ^ 2 } { y ^ 2 } = { S ^ 4 } – 4 { S ^ 2 } P. + 2 { P ^ 2 }. \ )
+ ) \ ( { x ^ 4 } + { y ^ 4 } + { x ^ 2 } { y ^ 2 } = ( { x ^ 2 } – xy + { y ^ 2 } ) ( { x ^ 2 } + xy + { y ^ 2 } ) = \ cdot \ cdot \ cdot \ )

c. Hệ phương trình đối xứng loại II

\( \bullet \)   Dấu hiệu nhận dạng: Khi thay đổi vị trí \(x\) và \(y\) cho nhau thì hệ phương trình không thay đổi và trật tự các phương trình thay đổi (phương trình này trở thành phương trình kia).

\( \bullet \)   Phương pháp giải:

– Bước 1 : Lấy vế trừ vế và nghiên cứu và phân tích thành nhân tử đưa về dạng \ ( ( x – y ). f ( x ) = 0, \ )
– Bước 2 : Tìm mối quan hệ giữa \ ( x, y \ ) từ phương trình thu được .

Chú ý:

– Ta luôn có \ ( x = y \ ) từ phương trình ở bước 1 .
– Từ mối quan hệ tìm được ở bước 2 ta đổi khác những phương trình đầu bài và giải nghiệm .

¬   Lưu ý: Đối với hệ đối xứng loại II chứa căn thức, sau khi trừ ta thường liên hợp.

d. Hệ phương trình đẳng cấp bậc hai

\( \bullet \)   Dạng tổng quát: \(\left\{ \begin{array}{l}{a_1}{x^2} + {b_1}xy + {c_1}{y^2} = {d_1}\\{a_2}{x^2} + {b_2}xy + {c_2}{y^2} = {d_2}\end{array} \right.\)                                    \((i)\)

\( \bullet \)   Phương pháp giải: \((i) \Leftrightarrow \left\{ \begin{array}{l}{d_2}({a_1}{x^2} + {b_1}xy + {c_1}{y^2}) = {d_1}.{d_2}\\{d_1}({a_2}{x^2} + {b_2}xy + {c_2}{y^2}) = {d_1}.{d_2}\end{array} \right.\)            \(\begin{array}{l}(1)\\(2)\end{array}\)

Lấy \ ( ( 1 ) – ( 2 ) \ Rightarrow ( { a_1 } { d_2 } – { a_2 } { d_1 } ) \ cdot { x ^ 2 } + ( { b_1 } { d_2 } – { b_2 } { d_1 } ) \ cdot xy + ( { c_1 } { d_2 } – { c_2 } { d_1 } ) \ cdot { y ^ 2 } = 0. \ ) Đây là phương trình đẳng cấp bậc hai nên sẽ tìm được mối liên hệ \ ( x, y \ )

¬   Lưu ý: Dạng \(\left\{ \begin{array}{l}{f_m}(x;y) = a\\{f_n}(x;y) = {f_k}(x;y)\end{array} \right.\) với \({f_m}(x;y),{\rm{ }}{f_n}(x;y),{\rm{ }}{f_k}(x;y)\) là các biểu thức đẳng cấp bậc \(m,{\rm{ }}n,{\rm{ }}k\) thỏa mãn \(m + n = k.\) Khi đó ta sẽ sử dụng kỹ thuật đồng bậc để giải.

Tức biến hóa hệ \ ( \ Leftrightarrow \ left \ { \ begin { array } { l } a = { f_m } ( x ; y ) \ \ a \ cdot { f_n } ( x ; y ) = a \ cdot { f_k } ( x ; y ) \ end { array } \ right. \ ) \ ( \ Rightarrow { f_m } ( x ; y ) \ cdot { f_n } ( x ; y ) = a. { f_k } ( x ; y ) \ ) và đây là phương trình quý phái bậc k.

Phần 4

Vectơ

1. Tổng, hiệu của hai vectơ

Các quy tắc:

Quy tắc ba điểm : Cho \ ( A, B, C \ ) tùy ý, ta có \ ( \ overrightarrow { AB } + \ overrightarrow { BC } = \ overrightarrow { AC } \ )
Quy tắc hình bình hành : Nếu \ ( ABCD \ ) là hình bình hành thì \ ( \ overrightarrow { AB } + \ overrightarrow { AD } = \ overrightarrow { AC } \ )

Ghi nhớ:

a ) Cho I là trung điểm của \ ( AB \ ) và \ ( M \ ) là một điểm nào đó, khi đó :
+ ) \ ( \ overrightarrow { IA } + \ overrightarrow { IB } = \ overrightarrow { 0. } \ )
+ ) \ ( \ overrightarrow { MA } + \ overrightarrow { MB } = 2 \ overrightarrow { MC } \ )
b ) Cho \ ( G \ ) là trọng tâm tam giác \ ( ABC \ ), \ ( M \ ) là một điểm bất kể. Khi đó :
+ ) \ ( \ overrightarrow { GA } + \ overrightarrow { GB } + \ overrightarrow { GC } = \ overrightarrow 0 \ )
+ ) \ ( \ overrightarrow { MA } + \ overrightarrow { MB } + \ overrightarrow { MC } = 3 \ overrightarrow { MG } \ )
Quy tắc về hiệu vectơ :
Nếu \ ( \ overrightarrow { MN } \ ) là một vectơ đã cho thì với điểm \ ( O \ ) bất kỳ ta luôn có \ ( \ overrightarrow { MN } = \ overrightarrow { ON } – \ overrightarrow { OM } \ )

2. Tích của véc tơ với một số

Tích của số \ ( k \ ne 0 \ ) với vectơ \ ( \ overrightarrow a \ ) : Nếu \ ( k \ ge 0 \ ) thì \ ( k \ overrightarrow a \ ) cùng hướng với \ ( \ overrightarrow a \ ) và độ dài \ ( \ left | { k \ overrightarrow a } \ right | = \ left | k \ right | \ left | { \ overrightarrow a } \ right | \ ), nếu \ ( k < 0 \ ) thì \ ( k \ overrightarrow a \ ) ngược hướng với \ ( \ overrightarrow a \ ) và \ ( \ left | { k \ overrightarrow a } \ right | = \ left | k \ right | \ left | { \ overrightarrow a } \ right | \ ) . Quy ước : \ ( 0. \ overrightarrow a = \ overrightarrow 0 ; k. \ overrightarrow 0 = \ overrightarrow 0 \ ) .

Tính chất:

Với hai vec tơ bất kể \ ( \ overrightarrow a, \ overrightarrow b \ ) và mọi số thực \ ( k, l \ ), ta có :
1 ) \ ( k \ left ( { l \ overrightarrow a } \ right ) = \ left ( { kl } \ right ) \ overrightarrow a \ )
2 ) \ ( \ left ( { k + l } \ right ) \ overrightarrow a = k \ overrightarrow a + l \ overrightarrow a \ )
3 ) \ ( k \ left ( { \ overrightarrow a + \ overrightarrow b } \ right ) = k \ overrightarrow a + k \ overrightarrow b \ ) ; \ ( k \ left ( { \ overrightarrow a – \ overrightarrow b } \ right ) = k \ overrightarrow a – k \ overrightarrow b \ )
4 ) \ ( k \ overrightarrow a = \ overrightarrow 0 \ Leftrightarrow k = 0 \ ) hoặc \ ( \ overrightarrow a = \ overrightarrow 0 \ )

Điều kiện để hai vectơ cùng phương:

\ ( \ overrightarrow b \ ) cùng phương với \ ( \ overrightarrow a \ left ( { \ overrightarrow a \ ne \ overrightarrow 0 } \ right ) \ Leftrightarrow \ exists k : \ overrightarrow b = k \ overrightarrow a \ )
Ba điểm \ ( A, B, C \ ) thẳng hàng \ ( \ Leftrightarrow \ exists k : \ overrightarrow { AB } = k \ overrightarrow { AC } \ ) .

Biểu thị một vectơ qua hai vectơ không cùng phương: Cho \(\overrightarrow a ,\overrightarrow b \) không cùng phương, \(\overrightarrow x \) là một vectơ tùy ý. Khi đó luôn tồn tại duy nhất cặp số \(m\) và \(n\) sao cho \(\overrightarrow x  = m\overrightarrow a  + n\overrightarrow b \).

Phương pháp nghiên cứu và phân tích một vectơ qua 2 vectơ không cùng phương : Sử dụng quy tắc ba điểm, quy tắc hình bình hành, đặc thù trung điểm, trọng tâm tam giác, tích 1 số ít với một vectơ để đổi khác .

Chú ý: Cho đoạn thẳng \(AB\), một điểm \(I \in AB\) thỏa mãn \(\overrightarrow {IA}  = k\overrightarrow {IB} \) thì với điểm \(M\) bất kì ta luôn có:

\ ( \ overrightarrow { MI } = \ dfrac { { – 1 } } { { k – 1 } } \ overrightarrow { MA } + \ dfrac { k } { { k – 1 } } \ overrightarrow { MB } \ )

3. Hệ trục tọa độ

– Hai vec tơ bằng nhau : \ ( \ overrightarrow a \ left ( { x ; y } \ right ) = \ overrightarrow b \ left ( { x ‘ ; y ‘ } \ right ) \ Leftrightarrow \ left \ { \ begin { array } { l } x = x ‘ \ \ y = y ‘ \ end { array } \ right. \ )
– Biểu thức tọa độ của những phép toán vec tơ :
– Cho \ ( \ overrightarrow a = \ left ( { x ; y } \ right ) \ ) và \ ( \ overrightarrow b = \ left ( { x ‘ ; y ‘ } \ right ) \ ). Khi đó
1 ) \ ( \ overrightarrow a + \ overrightarrow b = \ left ( { x + x ‘ ; y + y ‘ } \ right ) \ ) ; \ ( \ overrightarrow a – \ overrightarrow b = \ left ( { x – x ‘ ; y – y ‘ } \ right ) \ )
2 ) \ ( k \ overrightarrow a = \ left ( { kx ; ky } \ right ) \ ) với \ ( k \ in \ mathbb { R } \ )
3 ) \ ( \ overrightarrow b \ ) cùng phương với \ ( \ overrightarrow a \ ne \ overrightarrow 0 \ Leftrightarrow \ exists k : x ‘ = kx, y ‘ = ky \ ) .
– Với \ ( M ( { x_M } ; { y_M } ) ; N ( { x_N } ; { y_N } ) \ Rightarrow \ overrightarrow { MN } = \ left ( { { x_N } – { x_M } ; { y_N } – { y_M } } \ right ) \ )
– Nếu \ ( P \ ) là trung điểm của \ ( MN \ ) thì \ ( { x_P } = \ dfrac { { { x_M } + { x_N } } } { 2 } ; { y_P } = \ dfrac { { { y_M } + { y_N } } } { 2 } \ ) .
– Nếu G là trọng tâm tam giác \ ( ABC \ ) thì
\ ( { x_G } = \ dfrac { { { x_A } + { x_B } + { x_C } } } { 3 } ; { y_G } = \ dfrac { { { y_A } + { y_B } + { y_C } } } { 3 } \ ).

Phần 5

Tích vô hướng và ứng dụng

1. Giá trị lượng giác góc \(0^\circ  \le \alpha  \le 180^\circ \)

Tính chất:

\ ( \ begin { array } { l } \ sin \ left ( { 180 ^ \ circ – \ alpha } \ right ) = \ sin \ alpha \ \ \ cos \ left ( { 180 ^ \ circ – \ alpha } \ right ) = – \ cos \ alpha \ \ \ tan \ left ( { 180 ^ \ circ – \ alpha } \ right ) = – \ tan \ alpha \ left ( { \ alpha \ ne 90 ^ \ circ } \ right ) \ \ \ cot \ left ( { 180 ^ \ circ – \ alpha } \ right ) = – \ cot \ alpha \ left ( { 0 ^ \ circ < \ alpha < 180 ^ \ circ } \ right ) \ end { array } \ ) \ ( \ begin { array } { l } \ sin \ left ( { - \ alpha } \ right ) = - { \ mathop { \ rm s } \ nolimits } { \ rm { in } } \ alpha \ \ \ cos \ left ( { - \ alpha } \ right ) = \ cos \ alpha \ \ \ tan \ left ( { - \ alpha } \ right ) = - \ tan \ alpha \ left ( { \ alpha \ ne 90 ^ \ circ } \ right ) \ \ \ cot \ left ( { - \ alpha } \ right ) = - \ cot \ alpha \ left ( { 0 ^ \ circ < \ alpha < 180 ^ \ circ } \ right ) \ end { array } \ )

2. Tích vô hướng

Tích vô hướng của \ ( \ overrightarrow a \ ) và \ ( \ overrightarrow b \ ) : \ ( \ overrightarrow a. \ overrightarrow b = \ left | { \ overrightarrow a } \ right |. \ left | { \ overrightarrow b } \ right | \ cos \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) \ )

Tính chất: Với \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) tùy ý và mọi số thực \(k\), ta có:

1 ) \ ( { \ overrightarrow a ^ 2 } = { \ left | { \ overrightarrow a } \ right | ^ 2 } \ )
2 ) \ ( \ overrightarrow a. \ overrightarrow b = 0 \ Leftrightarrow \ overrightarrow a \ bot \ overrightarrow b \ )
3 ) \ ( \ left ( { k \ overrightarrow a } \ right ) \ overrightarrow b = \ overrightarrow a. \ left ( { k \ overrightarrow b } \ right ) = k \ left ( { \ overrightarrow a. \ overrightarrow b } \ right ) \ )
4 ) \ ( \ overrightarrow a \ left ( { \ overrightarrow b + \ overrightarrow c } \ right ) = \ overrightarrow a. \ overrightarrow b + \ overrightarrow a. \ overrightarrow c \ )
5 ) \ ( \ overrightarrow a \ left ( { \ overrightarrow b – \ overrightarrow c } \ right ) = \ overrightarrow a. \ overrightarrow b – \ overrightarrow a. \ overrightarrow c \ )

Các hệ thức quan trọng

Cho \ ( \ overrightarrow a = \ left ( { x ; y } \ right ) ; \ overrightarrow b = \ left ( { x ‘ ; y ‘ } \ right ) \ ). Khi đó
1 ) \ ( \ overrightarrow a. \ overrightarrow b = xx ‘ + yy ‘ \ )
2 ) \ ( \ left | { \ overrightarrow a } \ right | = \ sqrt { { x ^ 2 } + { y ^ 2 } } \ )
3 ) \ ( \ cos \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) = \ dfrac { { \ overrightarrow a. \ overrightarrow b } } { { \ left | { \ overrightarrow a } \ right |. \ left | { \ overrightarrow b } \ right | } } \ dfrac { { xx ‘ + yy ‘ } } { { \ sqrt { { x ^ 2 } + { y ^ 2 } } \ sqrt { x { ‘ ^ 2 } + y { ‘ ^ 2 } } } } \ left ( { \ overrightarrow a \ ne \ overrightarrow 0, \ overrightarrow b \ ne \ overrightarrow 0 } \ right ) \ )
4 ) \ ( \ overrightarrow a \ bot \ overrightarrow b \ Leftrightarrow xx ‘ + yy ‘ = 0 \ )
5 ) \ ( MN = \ sqrt { { { \ left ( { { x_N } – { x_M } } \ right ) } ^ 2 } + { { \ left ( { { y_N } – { y_M } } \ right ) } ^ 2 } } \ ) với \ ( M \ left ( { { x_M } ; { y_M } } \ right ), N \ left ( { { x_N }, { y_N } } \ right ) \ )

Hệ thức lượng trong tam giác và công thức diện tích

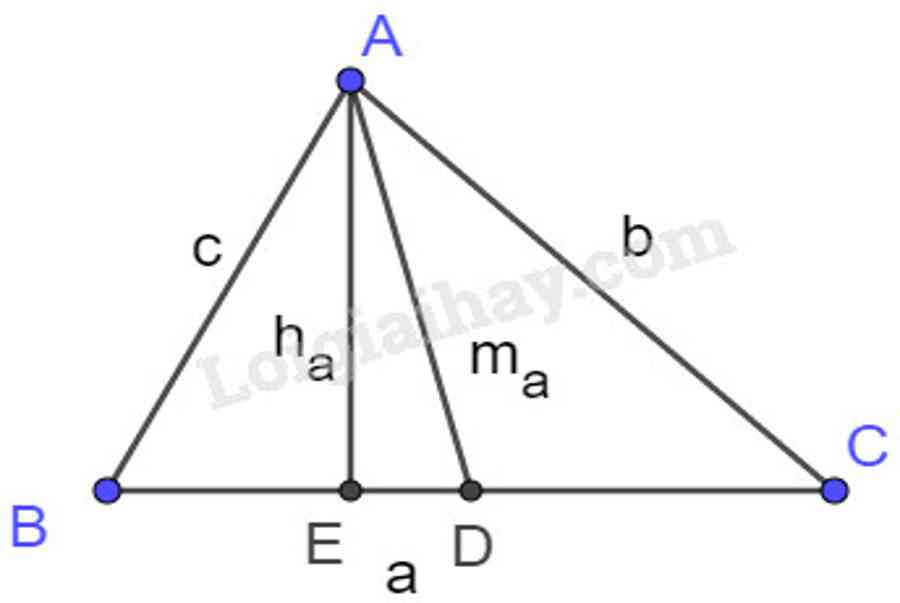
Cho tam giác \ ( ABC \ ) có \ ( a = BC ; b = AC ; c = AB ; R \ ) là nửa đường kính đường tròn ngoại tiếp \ ( \ Delta ABC \ ) ; \ ( r \ ) là nửa đường kính đường trong nội tiếp ; \ ( p = \ dfrac { { a + b + c } } { 2 } \ ) ; \ ( { h_a } \ ) là đường cao kẻ từ \ ( A \ ) ; \ ( { m_a } \ ) là trung tuyến kẻ từ \ ( A \ ) .

 

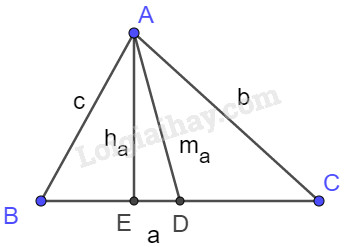
1 ) Định lí côsin trong tam giác : \ ( { a ^ 2 } = { b ^ 2 } + { c ^ 2 } – 2 bc \ cos A \ )
2 ) Định lí sin trong tam giác : \ ( \ dfrac { a } { { \ sin A } } = \ dfrac { b } { { \ sin B } } = \ dfrac { c } { { \ sin C } } = 2R \ )
3 ) Công thức trung tuyến : \ ( m_a ^ 2 = \ dfrac { { { b ^ 2 } + { c ^ 2 } } } { 2 } – \ dfrac { { { a ^ 2 } } } { 4 } \ )

4)    Công thức tính diện tích:

\ ( S = \ dfrac { 1 } { 2 } a { h_a } = \ dfrac { 1 } { 2 } ab \ sin C = \ dfrac { { abc } } { { 4R } } = pr = \ sqrt { p \ left ( { p – a } \ right ) \ left ( { p – b } \ right ) \ left ( { p – c } \ right ) } \ )

 Loigiaihay.com

Source: https://sangtaotrongtamtay.vn
Category: Giáo dục