Thiên văn học Hy Lạp cổ đại – Wikipedia tiếng Việt

Thiên văn học Hy Lạp cổ đại là nền thiên văn học được viết trong tiếng Hy Lạp vào thời cổ đại. Nền thiên văn học này bao gồm nền nền thiên văn học của Hy Lạp cổ đại, của thế giới Hy Lạp hóa, Hy-La và hậu kỳ sau đó. Nó không bị giới hạn về mặt địa lý trong khuôn khổ của Hy Lạp hay người Hy Lạp bởi vì tiếng Hy Lạp đã trở thành ngôn ngữ của giới học giả trong thế giới Hy Lạp hóa nằm trong các cuộc chinh phục của Alexander Đại đế. Vì thế, nền thiên văn học Hy Lạp cổ đại được biết đến với cái tên thiên văn học Hy Lạp hóa, trong khi đó nền thiên văn học trong tiếng Hy Lạp thuộc thời kỳ trước đó được gọi là thiên văn học Hy Lạp cổ điển. Dưới thời Hy Lạp hóa và thời La Mã, hầu hết các nhà thiên văn người Hy Lạp và không phải người Hy Lạp làm việc trong truyền thống của Hy Lạp, nghiên cứu ở Musaeum và thư viện Alexandria ở Ai Cập.

Sự tăng trưởng của thiên văn học của những nhà thiên văn học Hy Lạp và Hy Lạp hóa được xem xét bởi những nhà sử học là một hầu hết trong lịch sử dân tộc thiên văn học. Thiên văn học Hy Lạp đã được đặc tính hóa từ việc tìm ra cách lý giải mang đặc thù vật lý và tận gốc cho những hiện tượng kỳ lạ ngoài hành tinh. [ 1 ] Hầu như những chòm sao ở Bắc Bán cầu có nguồn gốc từ thiên văn học Hy Lạp. [ 2 ] Tên của nhiều ngôi sao 5 cánh, thiên thạch và hành tinh cũng xuất phát từ nền thiên văn học này. Thiên văn học Hy Lạp bị tác động ảnh hưởng bởi thiên văn học Ai Cập và thiên văn học Babylon. Đến lượt mình, nền thiên văn học Hy Lạp ảnh hưởng tác động đến thiên văn học Ấn Độ, thiên văn học Ả Rập và thiên văn học Tây Âu .

Thiên văn học Hy Lạp cổ xưa[sửa|sửa mã nguồn]

Anaximander

Tài liệu về các ngôi sao và chòm sao có thể được xác định đã xuất hiện trong các tác phẩm của Homer và Hesiod, những ví dụ mới nhất của nền văn minh Hy Lạp cổ đại. Trong những văn bản cổ nhất châu Âu, Iliad và Odyssey Homer đã đưa các hiện tượng thiên văn vào trong tác phẩm của mình, bao gồm các pha tối của Mặt Trời. Các pha tối này có thể cho phép việc định ra ngày tháng của những sự kiện trong những tác phẩm này, đồng thời việc tính toán thời gian trở nên có thể, đặc biệt là khi các hiện tượng vũ trụ xảy ra đồng thời.

Trong Iliad và Odyssey, Homer đã đề cập đến các vật thể vũ trụ sau:

Trong khi đó, Hesiod, tác giả trong đầu thế kỷ 7 TCN, đã thêm sao Arcturus trong lịch thơ Việc làm và Ngày. Mặc dù cả Homer và Hesiod đều không có tác phẩm khoa học, họ đã tạo ra một điểm nhấn sơ bộ của thiên hà học về Trái Đất phẳng được bao quanh bởi Sông Đại Dương. Một vài ngôi sao 5 cánh ngoi lên và lặn xuống ( biến mất trong biển trong cách nhìn của người Hy Lạp ), những ngôi sao 5 cánh khác là những chòm sao ở cực. Vào những thời gian xác lập của năm, những ngôi xác lập sẽ ngoi lên và lặn xuống cùng thời gian Mặt Trời mọc và lặn .Việc điều tra và nghiên cứu về ngoài hành tinh đã trở nên thông dụng trong triết học Tiền Socrates trong thế kỷ 6 TCN và thế kỷ 5 TCN. Anaximander ( 610 TCN – 546 TCN ) đã miêu tả một Trái Đất đi theo chu kỳ luân hồi lơ lửng trong TT của ngoài hành tinh và được bao quanh bởi những vòng lửa. Philolaus ( 480 TCN – 405 TCN ), một trong những người đã theo phe phái Pythagoras, đã miêu tả một ngoài hành tinh với sao, hành tinh, Mặt Trời, Mặt Trăng và Trái Đất và một phản Trái Đất có tên Antichthon, tổng thể đều quay quanh một vật thể không được nhìn thấy. Có những báo cáo giải trình đã chỉ ra rằng những nhà thiên văn học trong thế kỷ 6 và 5 TCN đã nhận ra sự Open của những hành tinh và suy đoán về cấu trúc của thiên hà. Đồng thời, có một miêu tả rất chi tiết cụ thể về thiên hà, Mặt Trời, Mặt Trăng, Trái Đất được tìm thấy trong Orphism, có niên đại vào cuối thế kỷ 5 TCN hoặc hoàn toàn có thể lâu hơn. Với những diễn đạt của những bài thơ Orphic tất cả chúng ta hoàn toàn có thể tìm được thông tin đáng kể cho rằng Trái Đất là hình cầu, nó có một trục giả tưởng và quay quanh cái trục đó trong vòng một ngày. Đồng thời, nó có 3 vùng khí hậu và Mặt Trời mê hoặc những ngôi sao 5 cánh và hành tinh. [ 3 ]

Các hành tinh trong thiên văn học Hy Lạp thời kỳ đầu[sửa|sửa mã nguồn]

Bức họa thời kỳ Phục hưng diễn đạt quy mô hai quả cầuKhái niệm ” hành tinh ” đến từ từ tiếng Hy Lạp πλανήτης ( planētēs ) có nghĩa là ” những người đi long dong “. Đồng thời những nhà thiên văn học cổ đại đã chú ý quan tâm rằng những tia sáng được xác lập của những hành tinh vận động và di chuyển nganng khung trời trong mối quan hệ với những ngôi sao 5 cánh khác. Năm hành tinh được nhìn thấy với mắ thường là : Thủy tinh, Kim tinh, Hỏa tinh, Mộc tinh và Thổ tinh. Những tên Hy Lap cho những hành tinh này là : Hermes, Aphrodite, Ares, Zeus và Cronus. Thỉnh thoảng những ngôi sao 5 cánh sáng, Mặt Trời và Mặt Trăng đã được thêm vào list những hành tinh hoàn toàn có thể được nhìn thấy bằng mắt thường để tạo ra một nhóm khá đầy đủ. Vì những hành tinh không Open trong khoảng chừng thời hạn mà Mặt Trời Open, người ta hay xác lập nhóm năm hành tinh được kể ở trên. Quan sát Kim tinh đã không mang đặc thù cởi mở. Những người Hy Lạp thời kỳ đầu đã nghĩ rằng đêm và ngày trên Kim tinh bộc lộ hai vật thể khác nhau, được gọi là sao hôm ( khi nó Open vào khung trời đêm ở phía tây ) và sao mai ( khi nó Open vào khung trời ngày ở phía đông ). Họ tiến tới nhận ra rằng cả hai vật thể này là cùng một hành tinh. Pythagoras được cho là một trong những người nhận ra điều này .

Trong Hy Lạp cổ điển, thiên văn học được xét đến là một ngành của toán học. Các nhà thiên văn học thời kỳ này mưu cầu một thiết kế ra những mô hình hình học có thể mô tả sư xuất hiện của các chuyển động vũ trụ. Truyền thống này đã bắt đầu với trường phái Pythagoras những người đã đặt thiên văn học vào một trong 4 môn nghệ thuật toán học (cùng với số học, hình học và âm nhạc). Những nghiên cứu về số bao gồm bốn lĩnh vực này sau này dược gọi là Quadrivium.

Mặc dù không phải là một nhà toán học, Plato (427 TCN – 347 TCN) đã thêm quadrivium như là nền tảng của giáo dục triết học trong tác phẩm Cộng hòa. Ông đã khuyến khích một nhà toán học trẻ tuổi hơn mình là Eudoxus (410 TCN – 347 TCN) để phát triển một hệ thống của thiên văn học Hy Lạp. Theo như nhà sử học hiện đại về khoa học David Lindberg: “Trong tác phẩm của hai người, chúng ta tìm được sự luân phiên của các ngôi sao trong mối quan tâm về các hánh tinh, sự sáng tạo của mô hình hình học, “mô hình hai quả cầu” đại diện cho các vì sao và các hiện tượng của các hành tinh, và sự tạo ra của tiêu chuẩn điều hành những lý thuyết được thiết kế dành cho những quan sát các hành tinh”.[4]

” Mô hình hai quả cầu ” là một quy mô hình học chia ngoài hành tinh thành hai khu vực, một là Trái Đất TT và bất động ( quả cầu con ) và một vương quốc quả cầu thiên đường lấy Trái Đất làm TT, hoàn toàn có thể gồm có nhiều quả cầu khác được là từ aether .

Cuốn sách chủ yếu của Plato về vũ trụ học là Timaeus và Cộng hòa. Ông đã mô tả mô hình hai quả cầu và nói rằng có 8 đường tròn hay hình cầu cho 7 hành tinh và các vì sao. Theo Huyền thoại Er trong cuốn Cộng hòa, vũ trụ là Trục chính của Sự cần thiết được điều hành bởi Sirens và được quay bởi ba người con gái của Chúa Cần thiết.

Theo như một câu chuyện được ghi lại bởi Simplicius (thế kỷ 6 TCN), Plato đã đặt một câu hỏi dành cho các nhà toán học đương thời: “Những chuyển động rõ ràng của các hành tinh có thể được giải thích bằng giả sử của những chuyển động có trật tự và đồng thời nào?” Plato đã dề xuất một chuyển động lang thang mất trật tự (có vẻ vậy) của các hành tinh có thể được giải thích băng sự kết hợp của những chuyển động vòng tròn đồng thời lấy Trái Đất làm trung tâm. Đây rõ ràng là một đề xuất mới lạ vào thế kỷ 4 TCN.

Eudoxus đã thúc đẩy sự thách thức bằng việc phân chia cho mỗi hành tinh một tập hợp của những quả cầu đồng tâm. Bằng việc đặt tên các trục của các quả cầu và phân chia mỗi một thời kỳ của một quá trình, ông có thể làm cho gần với “sự biểu diễn” vũ trụ. Vì thế, ông là người đầu tiên cố gắng có những mô tả toán học cho chuyển động của các hành tinh. Một ý kiến tổng quát trong tác phẩm Về Tốc độ, sách của ông về các hành tinh, có thể được lấy ý tưởng từ cuốn Siêu hình học của Aristotle và một bình luận của Simplicius về tác phẩm De caelo, một tác phẩm khác của Aristotle. Bởi vì các tác phẩm của Eudoxus đã bị mất, sự hiểu biết của chúng ta về ông chỉ được dựa vào những nguồn thứ hai. Bài thơ của Aratus về thiên văn học được dựa trên một tác phẩm của Eudoxus. Và có lẽ Sphaerics của Theodosius của Bithynia. Họ đưa ra một cái nhìn về các tác phẩm của Eudoxus về thiên văn học hình cầu cũng như những chuyển động của các hành tinh.

Callippus, một nhà thiên văn học người Hy Lạp vào thế kỷ 4 TCN, đã thêm 7 quả cầu vào mạng lưới hệ thống 27 quả cầu của Eudoxus ( ngoài những quả cầu hành tinh, Eudoxus đã thêm một quả cầu gồm nhiều ngôi sao 5 cánh ). Aristotle đã miêu tả những mạng lưới hệ thống này, nhưng nhấn mạnh vấn đề về việc thêm một quả cầu ” không quay ” giữa mỗi tập hợp những quả cầu để ngừng hoạt động của tập hợp bên ngoài. Aristotle được xem xét về tự nhiên vậy lý của mạng lưới hệ thống ; không có những thứ không quay, những hoạt động bên ngoài có thẻ dược chuyển vào những hoạt động bên trong .

Thiên văn học Hy Lạp hóa[sửa|sửa mã nguồn]

Mô hình những hành tinh và quan sát thiên văn[sửa|sửa mã nguồn]

Mô hình của Eudoxus đã có một vài điểm bị chỉ trích. Một trong những điểm đó là sự không thể của nó trong việc tiên đoán các chuyển động một cách chính xác. Công việc của Callippus có thể là một nỗ lực để sửa chữa điểm yếu này. Một vấn đề liên quan là sự không thể trong mô hình của Eudoxus tại sao các hành tinh xuất hiện để thay đổi tốc độ. Một điểm yếu thứ ba là sự không thể của nó trong việc giải thích sự thay đổi độ sáng của các hành tinh cũng như Trái Đất. Bpir vì những quả cầu đồng tâm, những hành tinh sẽ luôn duy trì cùng khoảng cách với Trái Đất. Vấn đề đã được nêu ra bởi tác phẩm Cổ xưa của Autolycus (Khoảng 310 TCN).

Apollonius ( khoảng chừng 262 TCN – khoảng chừng 192 TCN ) đã vấn đáp cho những yếu tố này bằng việc ra mắt hai kỹ thuật mới được cho phép một hành tinh hoàn toàn có thể đổi khác khoảng cách và vận tốc của nó : sự lệch tâm và ngoại luân và dẫn dắt. Cái để dẫn là một đường tròn mang những hành tinh xung quanh Trái Đất ( Từ ” để dẫn ” xuất phát từ tiếng Hy Lạp φέρω ( fero ) và tiếng Latin ferro, ferre ). Một cái dẫn lệch tâm là yếu ớt ở TT là Trái Đất. Trong một quy mô đường dẫn và ngoại luân, đường dẫn tạo ra một cái vòng tròn nhỏ hơn mang tên ngoại luân, đường tròn trở thành quỹ đạo của hành tinh. Mô hình này hoàn toàn có thể bắt chước quy mô ngoại luân và nó được gọi là định lý Apollonius. Nó hoàn toàn có thể lý giải sự giật lùi, thứ xảy ra khi những hành tinh Open đảo ngược hoạt động của nó trên cung hoàng đạo trong một khoảng chừng thời hạn ngắn. Các nhà sử học văn minh về thiên văn đã xác lập quy mô của Eudoxus hoàn toàn có thể chỉ gần tiếp cận sự giật lùi một cách sơ sài cho một vài hành tinh, không phải cho tổng thể .Trong thế kỷ 2 TCN, Hipparchus đã quan tâm về sự đúng đắn khác thường của thiên văn học Babylon hoàn toàn có thể tiên đoán hoạt động của những hành tinh và cho rằng những nhà thiên văn học Hy Lạp đang tiệm cận đến mức độ này. Vì lý dó này ông đã sử dụng những quan sát hoặc của những nhà thiên văn học Babylon để hoàn toàn có thể phong cách thiết kế những quy mô hình học tốt hơn. Về mặt trời, ông đã sử dụng một quy mô ngoại luân đơn thuần dựa trên những quan sát equinoxes, quy mô này đã lý giải được vận tốc của Mặt Trời và độ dài khác nhau của những mùa. Đối với Mặt Trăng, ông sử dụng một quy mô đường dẫn và ngoại luâ. Ông đã không hề phong cách thiết kế được những quy mô đúng mực cho những hành tinh đang sống sót và chỉ trích những nhà thiên văn học khác vì những quy mô không đúng mực của họ .Hipparchus cũng đã tạo ra một hạng mục sao. Theo như Pliny Cả, ông đã quan sát được một tân tinh. Vì vậy, những thế hệ sau hoàn toàn có thể nói những ngôi sao 5 cánh sẽ đi về đâu : chết, hoạt động, hay đổi khác ánh sáng. Hipparchus đã ghi lại vị trí và độ sáng của những vì sao. Ptolemy đã chú ý quan tâm rằng hạng mục này hạng mục này có liên hệ với tò mò tuế sai của chính Hipparchus ( Tuế sai của những equinoxes là hoạt động chậm khỏi vị trí khởi đầu trên đường hoàng đạo, được tạo ra bởi sự đổi khác về vị trí của trục Trái Đất ). Hipparchus đã nghĩ rằng tuế sai được tạo ra bởi sự hoạt động của quả cầu chứa những vì sao .

Thuyết nhật tâm và quy mô ngoài hành tinh[sửa|sửa mã nguồn]

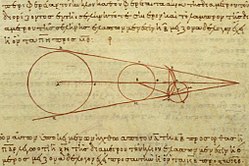Tính toán của Aristarchus về chu vi tương đối của Mặt Trời, Mặt Trăng và Trái Đất. Hình đến từ một bản soao chép từ thế kỷ 10

Trong thế kỷ 3 TCN, Aristarchus đã đề xuất vũ trụ học bổ sung (sự sắp xếp của vũ trụ): mô hình nhật tâm của hệ Mặt Trời, đặc Mặt Trời, không Trái Đất là trung tâm của vũ trụ được biết đến (vì vậy ông được nhớ đến như là “Copernicus của Hy Lạp). Ý tưởng của ông đã không được đón nhận rộng rãi và chỉ có một vài tham khảo nhỏ còn được lưu giữ. Một trong những người nối tiếp của Aristarchus là Seleucus.

Aristarchus đã viết một cuốn sách có tên Về Chu vi và Khoảng cách của Mặt Trời và Mặt Trăng, tác phẩm duy nhất của ông con tồn tại cho đến bây giờ. Trong tác phẩm này, ông đã tính toán kích thước của Mặt Trời và Mặt Trăng cũng như khoảng cách tới Trái Đất bằng Radii Trái Đất. Sau đó không lâu, Eratosthenes đã tính được chu vi của Trái Đất, cung cấp thêm một giá trị vào Radii Trái Đất có thể đã được sử dụng trong tính toán của Aristarchus. Hipparchus cũng đã viết một Về Chu vi và Khoảng cách của Mặt Trời và Mặt Trăng khác, rất tiếc là tác phẩm này không còn tồn tại. Cả Aristarchus và Hipparchus đã đánh giá thấp khoảng cách từ Mặt Trời đến Trái Đất.

Liên kết ngoài[sửa|sửa mã nguồn]

Source: https://sangtaotrongtamtay.vn
Category: Khoa học