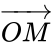Phép biến hình

Bởi

Phép biến hình là một quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với 1 và chỉ 1 điểm M.

Kí hiệu: f

Bạn đang đọc: Phép biến hình

Viết f ( M ) = M ‘ nghĩa là f biến M thành M ‘ ; M ‘ là ảnh của M qua f .

Các dạng phép biến hình

  • Phép tịnh tiến
  • Phép đối xứng trục
  • Phép đối xứng tâm
  • Phép quay
  • Phép vị tự
  • Phép dời hình
  • Phép đồng dạng

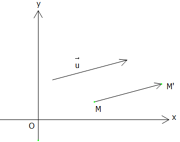
Phép tịnh tiến.png
Phép tịnh tiến theo vecto 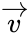{\displaystyle {\overrightarrow {v}}} là phép biến hình biến mỗi điểm M thành điểm M’ sao cho {\displaystyle {\overrightarrow {MM'}}} =
theo vectolà phép biến hình biến mỗi điểm M thành điểm M ‘ sao cho

Kí hiệu: T
T(M) = M’ <-> =

Nhận xét

  • Phép tịnh tiến hoàn toàn được xác định khi biết vecto tịnh tiến của nó.
  • Phép tịnh tiến theo {\displaystyle {\overrightarrow {0}}} là một phép đồng nhất.

Biểu thức tọa độ

M(x; y) —>[T với (a; b)] M'(x + a; y + b)

Tính chất

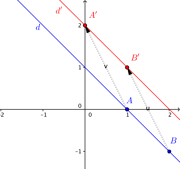
Phép tịnh tiến-tính chất.png
Định lí: Phép tịnh không làm thay đổi khoảng cách giữa hai điểm bất kì.
Phép tịnh không làm đổi khác khoảng cách giữa hai điểm bất kỳ .

Hệ quả:

  • Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự của các điểm tương ứng
  • Biến 1 tia thành 1 tia
  • Biến 1 đoạn thẳng thành 1 đoạn thẳng có độ dài bằng nó
  • Biến đường thẳng thành đường thẳng song song hoặc trùng với nó (Nếu vecto chỉ phương của đường thẳng cùng phương với vecto tịnh tiến thì biến đường thẳng thành đường thẳng trùng với nó; nếu vecto tịnh tiến không cùng phương với vecto chỉ phương của đường thẳng thì biến thành đường thẳng song song)
  • Biến 1 tam giác thành 1 tam giác bằng nó (trọng tâm, trực tâm, tâm đường tròn ngoại tiếp, nội tiếp biến thành các điểm tương ứng)
  • Biến 1 đường tròn thành đường tròn có cùng bán kính

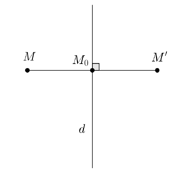
Phép đối xứng trục.png
Phép biến hình d là một phép biến hình biến mỗi điểm thuộc d thành chính nó; biến điểm M không thuộc d thành điểm M sao cho d là trung trực của MM’.
d là một phép biến hình biến mỗi điểm thuộc d thành chính nó ; biến điểm M không thuộc d thành điểm M sao cho d là trung trực của MM ‘ .

Kí hiệu: Đd(M) = M’

Biểu thức tọa độ

Phép đối xứng trục-tính chất.png

  • M(x;y) –>[ĐOx] M'(x;-y)
  • M(x;y) –>[ĐOy] M'(-x;y)

Tính chất

  • Biến đoạn thẳng thành đoạn thẳng có độ dài bằng nó
  • Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự giữa chúng
  • Biến 1 đường thẳng thành 1 đường thẳng
    • Đặc biệt: nếu trục d // Δ thì Δ’ // Δ; nếu trục d trùng Δ thì Δ’ trùng với Δ; nếu trục d cắt Δ tại điểm Y thì Δ’ cắt Δ tại Y; nếu d giao với Δ nhưng không vuông góc tại Y thì Δ’ giao với Δ tại Y; nếu d vuông góc với Δ thì Δ’ trùng với Δ)
  • Biến tam giác thành tam giác bằng nó
  • Biến 1 đường tròn thành đường tròn có cùng bán kính
  • Biến góc thành góc bằng nó

Định nghĩa trục đối xứng của một hình

  • Đường thẳng d gọi là trục đối xứng của hình (H) nếu như đối xứng trục d biến (H) thành chính nó

Phép đối xứng tâm.png
Phép đối xứng tâm O là phép biến hình biến điểm O thành chính nó; biến mỗi điểm M khác điểm O thành điểm M’ sao cho O là trung điểm của MM’.
tâm O là phép biến hình biến điểm O thành chính nó ; biến mỗi điểm M khác điểm O thành điểm M ‘ sao cho O là trung điểm của MM ‘ .

Kí hiệu: ĐO (M) = M’ <=> O là trung điểm của MM’

Nhận xét

Phép đối xứng tâm-tính chất.png

  • Điểm O gọi là tâm đối xứng của hình H nếu ĐO biến H thành chính nó.
Ví dụ: hình bình hành, hình thoi, hình chữ nhật, hình vuông, hình tròn có 1 tâm đối xứng

Biểu thức tọa độ

M(x;y) –>[ĐO với O(x0;y0)] M'(x’;y’) =>
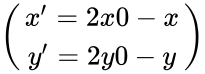
{ {\displaystyle {\begin{pmatrix}{x'=2x0-x}\\{y'=2y0-y}\end{pmatrix}}}

Tính chất

  • Bảo toàn khoảng cách giữa hai điểm bất kì
  • Biến 1 tia thành 1 tia
  • Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự của các điểm tương ứng
  • Biến 1 đoạn thẳng thành 1 đoạn thẳng có độ dài bằng nó
  • Biến đường thẳng thành đường thẳng song song hoặc trùng với nó (nếu tâm O nằm trên Δ thì Δ’ trùng với Δ; nếu tâm O không nằm trên Δ thì Δ’ // Δ)
  • Biến 1 góc thành góc bằng nó
  • Biến 1 tam giác thành tam giác bằng nó (trọng tâm, trực tâm, tâm đường tròn ngoại tiếp, nội tiếp biến thành các điểm tương ứng)
  • Biến 1 đường tròn thành đường tròn bằng nó (tâm biến thành tâm)

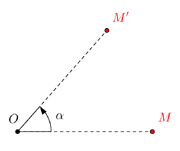
Phép quay.png
Phép quay tâm O góc α là một phép biến hình biến mỗi điểm M thành điểm M’ sao cho OM = OM’ và (OM, OM’) = α
tâm O góc α là một phép biến hình biến mỗi điểm M thành điểm M ‘ sao cho OM = OM ‘ và ( OM, OM ‘ ) = α

Kí hiệu: Q(O; α) (M) = M’ <=> 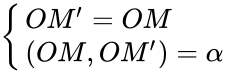{\displaystyle {\begin{cases}OM'=OM\\(OM,OM')=\alpha \end{cases}}}

Biểu thức của phép quay

M ( x ; y ), M ‘ ( x ‘ ; y ‘ )Q. ( 0 ; α ) ( M ) = M ‘

=>
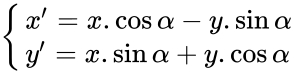
{\displaystyle {\begin{cases}x'=x.\cos \alpha -y.\sin \alpha \\y'=x.\sin \alpha +y.\cos \alpha \end{cases}}}

Nhận xét

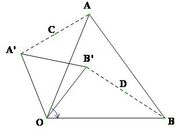
Phép quay-tính chất.jpg

  • Phép quay hoàn toàn xác định khi biết tâm và góc quay
  • chiều (+) của phép quay trùng với chiều (+) của đường tròn lượng giác
  • Phép quay với góc α = k2π là phép đồng nhất (biến mọi điểm M thành chính nó)
  • Phép quay với góc α = π + k2π là phép đối xứng tâm O

Tính chất

  • Biến đoạn thẳng thành đoạn thẳng có độ dài bằng nó
  • Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự giữa chúng
  • Biến tam giác thành tam giác bằng nó
  • Biến 1 đường tròn thành đường tròn có cùng bán kính
  • Biến góc thành góc bằng nó

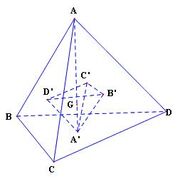
Phép vị tự.jpg
Phép vị tự tâm O tỉ số k là phép biến hình biến mỗi điểm M thành điểm M’ sao cho 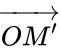{\displaystyle {\overrightarrow {OM'}}} bằng k lần {\displaystyle {\overrightarrow {OM}}}
tâm O tỉ số k là phép biến hình biến mỗi điểm M thành điểm M ‘ sao chobằng k lần

Kí hiệu: V(O;k) (M) = M’ <=> =k.

Biểu thức tọa độ

Nếu O ( x0 ; y0 ), M ( x ; y ), I ( a ; b ) thì V ( 0 ; k ) ( M ) = M ‘ ( x ‘ ; y ‘ )

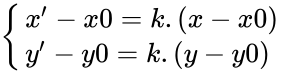
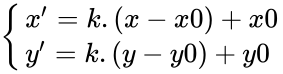
<=> {\displaystyle {\begin{cases}x'-x0=k.(x-x0)\\y'-y0=k.(y-y0)\end{cases}}} <=> {\displaystyle {\begin{cases}x'=k.(x-x0)+x0\\y'=k.(y-y0)+y0\end{cases}}}

Đặc biệt: Nếu O(0;0) thì {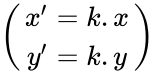{\displaystyle {\begin{pmatrix}x'=k.x\\y'=k.y\end{pmatrix}}}

Tính chất

Phép vị tự-tính chất.png

  • Phép vị tự tâm O tỉ số k biến M thành M’, N thành N’ thì {\displaystyle {\overrightarrow {M'N'}}}={\displaystyle k{\overrightarrow {MN}}}. Đoạn M’N’=|k|.MN
  • Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không thay đổi thứ tự giữa chúng
  • Biến 1 đường thẳng thành đường thẳng song song hoặc trùng với nó (nếu tâm vị tự 0 ∈ Δ hoặc tỉ số k=1 thì Δ’ trùng với Δ)
  • Biến 1 tia thành 1 tia
  • Biến một đoạn thẳng thành đoạn thẳng có độ dài gấp |k|
  • Biến một tam giác thành tam giác đồng dạng với nó
  • Biến góc thành góc bằng nó
  • Biến đường tròn bán kính R thành đường tròn có bán kính R’=|k.R|

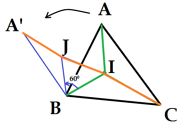
Phép dời hình.png
Phép dời hình là một phép biến hình không làm thay đổi khoảng cách giữa hai điểm bất kì.
là một phép biến hình không làm biến hóa khoảng cách giữa hai điểm bất kỳ .

Nhận xét

Các phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm, phép quay là những phép dời hình .

Tính chất

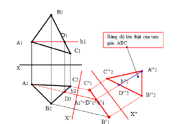
Phép dời hình-tính chất.png

  • Biến đoạn thẳng thành đoạn thẳng có độ dài bằng nó
  • Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự giữa chúng
  • Biến tam giác thành tam giác bằng nó
  • Biến 1 đường tròn thành đường tròn có cùng bán kính
  • Biến góc thành góc bằng nó
  • Khi thực hiện liên tiếp hai phép dời hình thì được một phép dời hình

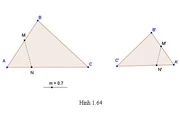
Phép đồng dạng.jpg
Phép biến hình f gọi là phép đồng dạng tỉ số k (k>0) nếu với hai điểm M và N bất kì và ảnh M’ và N’ của chúng, ta có đoạn M’N’=k.MN
Phép biến hình f gọi làtỉ số k ( k > 0 ) nếu với hai điểm M và N bất kể và ảnh M ‘ và N ‘ của chúng, ta có đoạn M’N ‘ = k. MN

Nhận xét

  • Các phép dời hình (phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm, phép quay) là các phép đồng dạng có tỉ số k=1. Phép vị tự là phép đồng dạng có tỉ số |k|
  • Phép đồng dạng không phải phép dời hình. Khi k=1 thì nó sẽ là phép dời hình

Tính chất

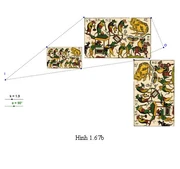
Phép đồng dạng-tính chất.jpg
–Định lí: Mọi phép dồng dạng đều là hợp thành của một phép vị tự và một phép dời hình

: Mọi phép dồng dạng đều là hợp thành của một phép vị tự và một phép dời hình

–Hệ quả:

  • Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự giữa chúng
  • Biến đường thẳng thành đường thẳng
  • Biến 1 tia thành 1 tia
  • Biến 1 đoạn thẳng thành đoạn thẳng có độ dài được nhân lên k lần
  • Biến một tam giác thành tam giác đồng dạng với tỉ số k
  • Biến đường tròn bán kính R thành đường tròn có bán kính R’=k.R

Định nghĩa hai hình đồng dạng

  • Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia

Tính chất

  • Phép tịnh tiến và phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó
  • Phép đối xứng trục và phép quay biến đường thẳng thành đường thẳng
  • Phép đối xứng tâm là phép vị tự có tỉ số k=-1
  • Phép vị tự là phép đồng nhất có tỉ số k=1
  • Mọi phép dời hình đều là phép đồng dạng với tỉ số k=1

Các bài viết liên quan

Viết một bình luận