Lực thủy triều – Wikipedia tiếng Việt

Bởi
An apparent force that stretches a body toàn thân towards and away from the center of mass of another body toàn thân due to a gradient in gravitational field Hình 1 : Sao chổi Shoemaker-Levy 9 năm 1994 sau khi bị phá vỡ bởi tác động ảnh hưởng của những lực thủy triều từ Sao Mộc trong lần bay ngang qua trước đó vào năm 1992 .

Lực thủy triều là một lực biểu kiến kéo giãn một vật thể về phía và ra xa khỏi khối tâm của một vật thể khác do gradien (khác biệt về cường độ) trong trường hấp dẫn từ vật thể kia; nó chịu trách nhiệm cho nhiều hiện tượng đa dạng, như thủy triều, khóa thủy triều, sự phá vỡ của các thiên thể và sự hình thành của các vành đai hành tinh trong phạm vi giới hạn Roche và trong những trường hợp tột cùng là hiện tượng mì ống hóa của các thiên thể. Nó sinh ra là do trường hấp dẫn tác động lên một vật thể bởi một vật thể khác không phải là một hằng số trong tất cả các bộ phận của nó: mặt gần nhất bị hấp dẫn mạnh hơn so với mặt xa nhất. Nó là chính là sự khác biệt làm cho vật thể bị kéo giãn. Vì thế, lực thủy triều còn được biết đến như là lực vi phân, cũng như là hiệu ứng thứ cấp của trường hấp dẫn.

Trong cơ học thiên thể, biểu hiện của lực thủy triều có thể là chỉ tới tình huống khi một vật thể hay một khối vật chất (chẳng hạn nước thủy triều) chủ yếu chịu ảnh hưởng hấp dẫn của một vật thể thứ hai (chẳng hạn Trái Đất), nhưng cũng bị gây nhiễu bởi các tác động hấp dẫn của vật thể thứ ba (chẳng hạn Mặt Trăng). Lực gây nhiễu trong những trường hợp như vậy đôi khi gọi là lực thủy triều[1] (chẳng hạn lực gây nhiễu lên Mặt Trăng): nó là sự khác biệt giữa lực tác động bởi vật thể thứ ba lên vật thể thứ hai và lực tác động bởi vật thể thứ ba lên vật thể thứ nhất.[2]

Lực mê hoặc và cường độ trường mê hoặc[sửa|sửa mã nguồn]

Lực mê hoặc không giống hệt với trường mê hoặc .

Trường hấp dẫn trải rộng trong không gian xung quanh một vật thể có khối lượng và sinh ra lực hấp dẫn lên các vật thể có khối lượng khác, phụ thuộc vào khoảng cách và khối lượng của các vật thể này.[3] Cường độ của trường hấp dẫn giảm tỷ lệ nghịch với bình phương khoảng cách từ vật thể có khối lượng.

Lực thủy triều không phải là một lực mà là sự khác biệt trong cường độ trường hấp dẫn.

Kích thước và khoảng cách[sửa|sửa mã nguồn]

Mối quan hệ của kích cỡ của một thiên thể với khoảng cách của nó từ một vật thể khác tác động ảnh hưởng mạnh tới độ lớn của lực thủy triều. [ 4 ] Lực thủy triều ảnh hưởng tác động lên một thiên thể, như Trái Đất, tỷ suất thuận với đường kính của thiên thể đó và tỷ suất nghịch với lập phương khoảng cách từ thiên thể khác sinh ra sức hút mê hoặc, như Mặt Trăng hay Mặt Trời ( Xem giải thích dưới đây ). Tác động thủy triều lên những bể tắm, hồ bơi, hồ nước và những vật thể nhỏ chứa nước khác là không đáng kể. [ 5 ]
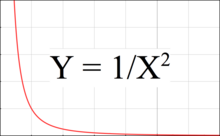Hình 3 : Đồ thị chỉ ra sức hút mê hoặc từ một vật thể giảm xuống khi khoảng cách tăng lên như thế nào .Hình 3 là đồ thị chỉ ra sự giảm xuống của lực mê hoặc theo khoảng cách tăng lên. Trong đồ thị này, lực mê hoặc giảm tỷ suất với bình phương khoảng cách trong khi gradien ( độ dốc ) giảm tỷ suất theo khoảng cách. Điều này giải thích tại sao gradien ở điểm bất kể là tỷ suất nghịch theo lập phương khoảng cách .Lực thủy triều tương ứng với độc lạ trong Y giữa hai điểm trên đồ thị, với một điểm ở mặt gần của vật thể, và một điểm khác ở mặt xa của vật thể. Lực thủy triều trở nên lớn hơn khi 2 điểm hoặc là xa nhau hơn hoặc là khi chúng là nằm gần về bên trái hơn của đồ thị, nghĩa là gần hơn với vật thể mê hoặc .Chẳng hạn lực thủy triều lên Trái Đất do Mặt Trăng sinh ra lớn hơn so với do Mặt Trời sinh ra, mặc dầu ảnh hưởng tác động mê hoặc lên Trái Đất do Mặt Trời sinh ra lớn hơn so với do Mặt Trăng sinh ra, là do gradien là nhỏ hơn. Mặt Trăng sinh ra lực thủy triều lớn hơn lên Trái Đất so với lực thủy triều do Trái Đất sinh ra tác động ảnh hưởng lên Mặt Trăng. Khoảng cách là như nhau nhưng đường kính của Trái Đất lớn hơn của Mặt Trăng làm cho lực thủy triều cũng lớn hơn .Điều xảy ra không phải là tổng sức hút mê hoặc lên vật thể mà là sự độc lạ mê hoặc từ bên này sang bên kia. Đường kính của vật thể càng lớn thì độc lạ từ bên này sang bên kia càng lớn. [ 6 ]Sức hút mê hoặc tỷ suất nghịch với bình phương khoảng cách từ nguồn. Sức hút sẽ là mạnh hơn ở bên của vật thể đối lập với nguồn và yếu hơn ở bên xa nguồn. Lực thủy triều là tỷ suất thuận với sự độc lạ. [ 5 ]
vi phân hấp dẫn của Mặt Trăng tại bề mặt Trái Đất (cùng với hiệu ứng vi phân khác nhưng yếu hơn từ Mặt Trời) được biết đến như là lực phát sinh thủy triều. Đây là cơ chế chính dẫn dắt tác động thủy triều, giải thích 2 chỗ phồng bên ngoài của các mũi tên ở bên trái và bên phải chỉ ra rằng nơi mà Mặt Trăng hoặc là ở Hình 4 : Trườnghấp dẫn của Mặt Trăng tại bề mặt Trái Đất ( cùng với hiệu ứng vi phân khác nhưng yếu hơn từ Mặt Trời ) được biết đến như là lực phát sinh thủy triều. Đây là chính sách chính dẫn dắt ảnh hưởng tác động thủy triều, giải thích 2 chỗ phồng đẳng thế thủy triều, và giải thích cho 2 triều cao mỗi ngày. Trong hình này, Trái Đất là hình tròn trụ màu xanh lam ở TT trong khi Mặt Trăng nằm xa bên ngoài phía bên phải. Các hướng racủa những mũi tên ở bên trái và bên phải chỉ ra rằng nơi mà Mặt Trăng hoặc là ở thiên đỉnh hoặc là ở thiên để ) thì lực gây nhiễu của nó là ngược lại với lực giữa Trái Đất và đại dương .

Khi một vật thể (vật thể 1) chịu tác động bởi hấp dẫn của một vật thể khác (vật thể 2), trường có thể thay đổi đáng kể trên vật thể 1 giữa bên của vật thể 1 đối mặt với vật thể 2 và bên của vật thể 1 nằm xa vật thể 2. Hình 4 chỉ ra lực vi phân của hấp dẫn trên một vật thể hình cầu (vật thể 1) do một vật thể khác (vật thể 2) gây ra. Cái gọi là lực hấp dẫn gây ra các sức căng trên cả hai vật thể và có thể làm biến dạng chúng hoặc thậm chí trong các trường hợp tột cùng có thể phá vỡ vật thể này hay vật thể kia.[7] Giới hạn Roche là khoảng cách từ một hành tinh mà từ đó các tác động thủy triều có thể làm cho một vật thể bị tan rã do lực vi phân của hấp dẫn từ hành tinh lớn hơn sức hút của các bộ phận của vật thể với nhau.[6] Các sức căng này sẽ không diễn ra nếu trường hấp dẫn là đồng nhất, do một trường đồng nhất chỉ làm cho một vật thể liền khối gia tốc cùng nhau theo cùng một hướng và cùng một tốc độ.

Xử lý toán học[sửa|sửa mã nguồn]

[8]Hình 5 : Lực thủy triều chịu nghĩa vụ và trách nhiệm cho sự hợp nhất của cặp thiên hà MRK 1034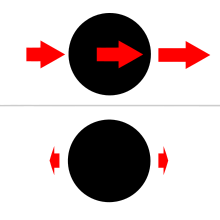 Hình 6 : Đồ thị minh họa lực thủy triều. Hình trên chỉ ra trường mê hoặc của một vật thể ở bên phải, hình dưới chỉ ra phần dư còn lại của nó sau khi trường ở TT hình cầu được trừ đi ; đó chính là lực thủy triều. Xem Hình 4 để biết thêm cụ thể .

Đối với một trường hấp dẫn phát sinh bên ngoài đã cho, gia tốc thủy triều tại một điểm đối với một vật thể thu được cách trừ vectơ gia tốc hấp dẫn tại tâm vật thể (do trường phát sinh ngoài đã cho) khỏi gia tốc hấp dẫn (do cùng trường này sinh ra) tại điểm đã cho. Tương ứng, thuật ngữ lực thủy triều được sử dụng để mô tả các lực do gia tốc thủy triều. Lưu ý rằng đối với các mục đích này trường hấp dẫn duy nhất được xem xét là là trường bên ngoài; trường hấp dẫn của vật thể đó (như chỉ ra trong đồ thị) là không liên quan (Nói cách khác, sự so sánh là với các điều kiện tại điểm đã cho như chúng có thể sẽ là vậy nếu không có trường phát sinh ngoài tác động không đều tại điểm đã cho và tại tâm của vật thể tham chiếu. Trường phát sinh ngoài thường là trường tạo ra bởi vật thể thứ ba gây nhiễu, thông thường là Mặt Trăng hay Mặt Trời đối với các điểm trên bề mặt Trái Đất trong hệ tham chiếu địa tâm).

Gia tốc thủy triều không nhu yếu sự tự quay hay những vật thể đang quay ; ví dụ điển hình vật thể hoàn toàn có thể rơi tự do theo một đường thẳng dưới ảnh hưởng tác động của trường mê hoặc trong khi vẫn chịu ảnh hưởng tác động bởi tần suất thủy triều ( biến hóa ) .

Theo Định luật vạn vật hấp dẫn của Newton và các định luật về chuyển động, một vật thể với khối lượng m ở khoảng cách R từ tâm của một khối cầu với khối lượng M chịu một lực

F
→

g

{\displaystyle {\vec {F}}_{g}}

{\displaystyle {\vec {F}}_{g}},

F → g = − r ^ G M m R 2 { \ displaystyle { \ vec { F } } _ { g } = – { \ hat { r } } ~ G ~ { \ frac { Mm } { R ^ { 2 } } } }{\displaystyle {\vec {F}}_{g}=-{\hat {r}}~G~{\frac {Mm}{R^{2}}}}

tương đương gia tốc

a
→

g

{\displaystyle {\vec {a}}_{g}}

{\displaystyle {\vec {a}}_{g}},

a → g = − r ^ G M R 2 { \ displaystyle { \ vec { a } } _ { g } = – { \ hat { r } } ~ G ~ { \ frac { M } { R ^ { 2 } } } }{\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}}

trong đó

r
^

{\displaystyle {\hat {r}}}

{\displaystyle {\hat {r}}} là đơn vị vectơ có hướng từ vật thể M tới vật thể m (ở đây gia tốc từ m về phía M có dấu âm).

Xét gia tốc do khối cầu khối lượng M mà một hạt gần với vật thể khối lượng m phải chịu. Với R là khoảng cách từ tâm M tới tâm m, đặt ∆r (tương đối nhỏ) là khoảng cách của hạt từ tâm vật thể khối lượng m. Để đơn giản hóa, các khoảng cách chỉ được xem xét theo hướng về phía hoặc ra xa khỏi khối cầu khối lượng M. Nếu vật thể khối lượng m là một khối cầu bán kính ∆r thì hạt mới đang xem xét có thể nằm trên bề mặt khối cầu khối lượng m, ở khoảng cách R ± ∆r từ tâm của khối cầu khối lượng M và ∆r có thể là dương khi khoảng cách của hạt từ M lớn hơn R. Bỏ qua gia tốc hấp dẫn mà hạt phải chịu về phía m vì khối lượng của chính m, ta có gia tốc lên hạt do lực hấp dẫn về phía M là:

a
→

g

=
−

r
^

 
G
 

M

(
R
±
Δ
r

)

2

{\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{(R\pm \Delta r)^{2}}}}

{\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{(R\pm \Delta r)^{2}}}}

Rút R2 ra khỏi mẫu số ta có:

a → g = − r ^ G M R 2 1 ( 1 ± Δ r R ) 2 { \ displaystyle { \ vec { a } } _ { g } = – { \ hat { r } } ~ G ~ { \ frac { M } { R ^ { 2 } } } ~ { \ frac { 1 } { \ left ( 1 \ pm { \ frac { \ Delta r } { R } } \ right ) ^ { 2 } } } }{\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}~{\frac {1}{\left(1\pm {\frac {\Delta r}{R}}\right)^{2}}}}

Chuỗi Maclaurin của

1

/

(
1
±
x

)

2

{\displaystyle 1/(1\pm x)^{2}}

{\displaystyle 1/(1\pm x)^{2}} là

1
∓
2
x
+
3

x

2

∓
⋯

{\displaystyle 1\mp 2x+3x^{2}\mp \cdots }

{\displaystyle 1\mp 2x+3x^{2}\mp \cdots } cho ta biểu thức:

a → g = − r ^ G M R 2 ± r ^ G 2 M R 2 Δ r R + ⋯ { \ displaystyle { \ vec { a } } _ { g } = – { \ hat { r } } ~ G ~ { \ frac { M } { R ^ { 2 } } } \ pm { \ hat { r } } ~ G ~ { \ frac { 2M } { R ^ { 2 } } } ~ { \ frac { \ Delta r } { R } } + \ cdots }{\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}\pm {\hat {r}}~G~{\frac {2M}{R^{2}}}~{\frac {\Delta r}{R}}+\cdots }

Số hạng thứ nhất là gia tốc hấp dẫn do M gây ra tại tâm của khối tham chiếu

m

{\displaystyle m}

m, nghĩa là tại điểm mà

Δ
r

{\displaystyle \Delta r}

{\displaystyle \Delta r} bằng 0. Số hạng này không ảnh hưởng tới gia tốc được quan sát của các hạt trên bề mặt m do đối với M thì m (và mọi thứ trên bề mặt nó) là rơi tự do. Khi lực lên hạt ở phía xa trừ đi lực lên hạt ở gần (hay ngược lại) thì số hạng đầu tiên này đều bị triệt tiêu, cũng như tất cả các số hạng có bậc chẵn khác. Các số hạng còn lại chính là khác biệt đề cập trên đây và là các số hạng của lực thủy triều (gia tốc). Khi ∆r là nhỏ so với R thì các số hạng sau số hạng còn lại đầu tiên là rất rất nhỏ và có thể bỏ qua, nên gia tốc thủy triều gần đúng là

a
→

t
,

axial

{\displaystyle {\vec {a}}_{t,{\text{axial}}}}

{\displaystyle {\vec {a}}_{t,{\text{axial}}}} đối với khoảng cách ∆r được xem xét, dọc theo trục nối các tâm của m và M:

a → t, axial ≈ ± r ^ 2 Δ r G M R 3 { \ displaystyle { \ vec { a } } _ { t, { \ text { axial } } } \ approx \ pm { \ hat { r } } ~ 2 \ Delta r ~ G ~ { \ frac { M } { R ^ { 3 } } } }{\displaystyle {\vec {a}}_{t,{\text{axial}}}\approx \pm {\hat {r}}~2\Delta r~G~{\frac {M}{R^{3}}}}

Khi tính toán theo cách này cho trường hợp khi ∆r là khoảng cách dọc theo trục nối các tâm m và M,

a
→

t

{\displaystyle {\vec {a}}_{t}}

{\displaystyle {\vec {a}}_{t}} có hướng ra ngoài từ tâm của m (nơi ∆r bằng 0).

Các gia tốc thủy triều cũng có thể tính cho các điểm nằm ngoài trục nối tâm các vật thể m và M dựa theo tính toán vectơ. Trong mặt phẳng vuông góc với trục nối tâm, gia tốc thủy triều có hướng vào trong (về phía tâm nơi ∆r bằng 0), và biên độ của nó bằng

1
2

|

a
→

t
,

axial

|

{\textstyle {\frac {1}{2}}\left|{\vec {a}}_{t,{\text{axial}}}\right|}

{\textstyle {\frac {1}{2}}\left|{\vec {a}}_{t,{\text{axial}}}\right|} trong xấp xỉ tuyến tính như trong Hình 4.

Các gia tốc thủy triều tại bề mặt các hành tinh trong hệ Mặt Trời nói chung là rất nhỏ. Chẳng hạn, tgia tốc thủy triều mặt trăng tại bề mặt Trái Đất dọc theo trục Mặt Trăng-Trái Đất chỉ khoảng 1,1 × 10−6 g, trong khi gia tốc thủy tiều mặt trời tại bề mặt Trái Đất dọc theo trục Mặt Trời-Trái Đất chỉ khoảng 0,52 × 10−6 g, trong đó g là gia tốc hấp dẫn tại bề mặt Trái Đất (9,80665 m/s2). Vì thế, lực dâng (gia tốc) thủy triều do Mặt Trời chỉ bằng khoảng 45% lực dâng thủy triều do Mặt Trăng.[9] Gia tốc thủy triều mặt trời tại bề mặt Trái Đất được Newton tính đầu tiên trong Philosophiæ Naturalis Principia Mathematica.[10]

Mặt Trời, Trái Đất, Mặt Trăng[sửa|sửa mã nguồn]

Như giải thích trên đây, bảng sau chỉ ra khoảng cách từ Mặt Trăng tới Trái Đất là bằng khoảng cách từ Trái Đất tới Mặt Trăng. Trái Đất nặng hơn Mặt Trăng 81 lần nhưng có nửa đường kính lớn hơn 3,7 lần. Do đó, dù cùng khoảng cách nhưng lực thủy triều lên mỗi đơn vị chức năng khối lượng của Trái Đất lên Mặt Trăng là khoảng chừng 22 lần mạnh hơn lực thủy triều lên mỗi đơn vị chức năng khối lượng của Mặt Trăng lên Trái Đất. Vì thế Trái Đất hoàn toàn có thể khóa quỹ đạo của Mặt Trăng là quay xung quanh Trái Đất nhưng không phải là ngược lại .

Vật thể hấp dẫn sinh ra lực thủy triều
Vật thể chịu tác động lực thủy triều
Đường kính và khoảng cách
Lực thủy triều trên đơn vị khối lượng

Vật thể
Khối lượng (m)
Vật thể
Bán kính (r)
Khoảng cách (d)
2 r d 3 { \ displaystyle { \ frac { 2 r } { d ^ { 3 } } } }{\displaystyle {\frac {2r}{d^{3}}}}
G m 2 r d 3 { \ displaystyle ~ Gm ~ { \ frac { 2 r } { d ^ { 3 } } } }{\displaystyle ~Gm~{\frac {2r}{d^{3}}}}
Mặt Trời
1,99E+30
Trái Đất
6,37E+06
1,50E+11
3,81E-27
5,05E-07

Mặt Trăng
7,34E+22
Trái Đất
6,37E+06
3,84E+08
2,25E-19
1,10E-06

Trái Đất
5,97E+24
Mặt Trăng
1,74E+06
3,84E+08
6,14E-20
2,45E-05

m là khối lượng tính bằng kilogam; r là bán kính tính bằng mét, đường kính = 2r; d là khoảng cách tính bằng mét; G là hằng số hấp dẫn =

66740831×10−11 N•kg–2•m2

Tác động của lực thủy triều[sửa|sửa mã nguồn]

[11]Hình 7 : Vành đai Sao Thổ nằm bên trong quỹ đạo những vệ tinh chính của nó. Lực thủy triều ngược lại với sự hợp nhất mê hoặc của vật chất trong vành đai để tạo thành những vệ tinh .Trong trường hợp một vật thể hình cầu đàn hồi kích cỡ vô cùng nhỏ, ảnh hưởng tác động của lực thủy triều là làm biến dạng vật thể mà không làm biến hóa thể tích của nó. Hình cầu này trở thành một ellipxoit với 2 chỗ phồng lên, hướng về và hướng ra xa vật thể gây mê hoặc. Các vật thể lớn hơn bị biến dạng thành hình trứng ( ovoid ), và hơi bị ép dẹp xuống, như những gì xảy ra với những đại dương của Trái Đất dưới ảnh hưởng tác động của Mặt Trăng. Hệ Trái Đất – Mặt Trăng quay xung quanh khối tâm chung của hệ ( khối tâm hệ thiên thể ), và sức hút mê hoặc của chúng tạo ra lực hướng tâm thiết yếu để duy trì hoạt động này. Đối với người quan sát trên Trái Đất, rất gần với khối tâm hệ thiên thể này, trường hợp là Trái Đất như thể vật thể 1 chịu tác động ảnh hưởng mê hoặc của Mặt Trăng như là vật thể 2. Tất cả những phần của Trái Đất đều chịu tác động ảnh hưởng của lực mê hoặc từ Mặt Trăng, làm cho nước trong những đại dương phân bổ lại, tạo ra những chỗ phồng lên ở những bên gần nhất và xa nhất với Mặt Trăng. [ 12 ]Khi một vật thể tự quay trong khi chịu tác động ảnh hưởng của lực thủy triều thì ma sát bên trong nó tạo ra sự hao tán từ từ động năng tự quay của nó dưới dạng nhiệt. Trong trường hợp Trái Đất và Mặt Trăng thì tổn thất động năng tự quay gây ra sự tăng thêm chu kỳ luân hồi tự quay khoảng chừng khoảng chừng 2 mili giây mỗi thế kỷ. Nếu vật thể đủ gần với vật thể chính của hệ, điều này hoàn toàn có thể làm cho hoạt động tự quay bị khóa thủy triều với hoạt động quay trên quỹ đạo, như trong trường hợp của Mặt Trăng. Sấy nóng thủy triều tạo ra những hiệu ứng núi lửa kinh hoàng trên vệ tinh Io của Sao Mộc. Ứng suất gây ra bởi những lực thủy triều cũng gây ra quy mô chấn động thiên thể chu kỳ luân hồi đều hàng tháng trên Mặt Trăng. [ 4 ]Các lực thủy triều cũng góp thêm phần vào những hải lưu, điều hòa nhiệt độ toàn thế giới bằng việc luân chuyển nhiệt năng tới hai cực. Người ta cũng từng yêu cầu rằng ngoài những yếu tố khác thì những dịch chuyển phách điều hòa trong lực thủy triều cũng hoàn toàn có thể góp thêm phần vào đổi khác khí hậu. Tuy nhiên, cho tới nay người ta vẫn chưa tìm thấy mối link đủ mạnh chứng minh điều này. [ 13 ]

Các hiệu ứng thủy triều trở nên đặc biệt rõ ràng khi gần các vật thể nhỏ với khối lượng lớn, như các sao neutron hay các lỗ đen, nơi mà chúng chịu trách nhiệm cho cái gọi là “mì ống hóa” vật chất đang rơi vào. Các lực thủy triều tạo ra thủy triều trên các đại dương của Trái Đất, nơi mà vật thể hấp dẫn chính là Mặt Trăng và ở mức độ nhỏ hơn là Mặt Trời. Các lực thủy triều chịu trách nhiệm cho khóa thủy triều, gia tốc thủy triều và sấy nóng thủy triều. Thủy triều cũng có thể kích hoạt các trận động đất.

Bằng việc sinh ra những dòng chất lưu có tính dẫn điện bên trong Trái Đất, những lực thủy triều cũng tác động ảnh hưởng tới từ trường Trái Đất. [ 14 ]

Liên kết ngoài[sửa|sửa mã nguồn]

Các bài viết liên quan

Viết một bình luận